题目内容
如图,正比例函数y=mx和反比例函数y=| n | x |
 比例函数的图象上.
比例函数的图象上.(1)求正比例函数和反比例函数的解析式;
(2)过A点作直线AD与x轴交于点D,且△AOD的面积为3,求点D的坐标.
分析:(1)根据点B(2,1)在反比例函数的图象上求出n的值,再求出a的值,又知A点在正比例函数的图象上,即可求出m的值,
(2)首先根据反比例函数的性质和△AOD的面积为3等条件,求出OD的长,再求D点的坐标.
(2)首先根据反比例函数的性质和△AOD的面积为3等条件,求出OD的长,再求D点的坐标.
解答: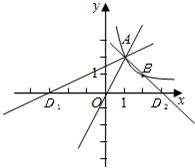 解:(1)∵反比例函数y=
解:(1)∵反比例函数y=
的图象经过点B(2,1),
∴n=2.
∴反比例函数的解析式是y=
.(1分)
∵点A(1,a)在反比例函数y=
的图象上,
∴a=2.
∴A(1,2).(2分)
∵正比例函数y=mx的图象经过点A(1,2),
∴m=2.
∴正比例函数的解析式是y=2x.(3分)
(2)依题意,得
×OD×2=3,
∴OD=3,
∴D点坐标为(-3,0)或(3,0).(5分)
 解:(1)∵反比例函数y=
解:(1)∵反比例函数y=| n |
| x |
∴n=2.
∴反比例函数的解析式是y=
| 2 |
| x |
∵点A(1,a)在反比例函数y=
| 2 |
| x |
∴a=2.
∴A(1,2).(2分)
∵正比例函数y=mx的图象经过点A(1,2),
∴m=2.
∴正比例函数的解析式是y=2x.(3分)
(2)依题意,得
| 1 |
| 2 |
∴OD=3,
∴D点坐标为(-3,0)或(3,0).(5分)
点评:本题主要考查反比例函数与一次函数的交点问题和待定系数法求函数解析式的知识点,解答本题的突破口是利用数形结合进行解题,充分利用反比例函数的性质,本题是一道比较不错的习题.

练习册系列答案
相关题目
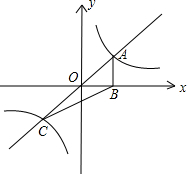 如图,正比例函数y=kx(k>0)与反比例函数y=
如图,正比例函数y=kx(k>0)与反比例函数y=| 1 |
| x |
| A、S=1 | B、S=2 |
| C、S=3 | D、S的值不能确定 |
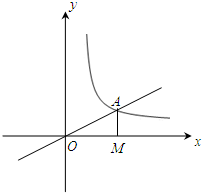 如图,正比例函数
如图,正比例函数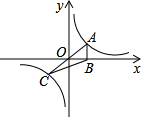 如图,正比例函数y=kx(k>0)与反比例函数y=
如图,正比例函数y=kx(k>0)与反比例函数y= 作x轴的垂线,垂足为M,已知△AOM的面积为1,点B(-1,t)为反比例函数在第三象限图象上的点.
作x轴的垂线,垂足为M,已知△AOM的面积为1,点B(-1,t)为反比例函数在第三象限图象上的点. 已知:如图,正比例函数y=k1x的图象与反比例函数
已知:如图,正比例函数y=k1x的图象与反比例函数