题目内容
下面是某同学对多项式(x2—4x+2)(x2—4x+6)+4进行分解因式的过程。
解:设x2—4x=y.
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2 (第三步)
=(x2—4x+4)2 (第四步)
回答下列问题:
(1)该同学第二步到第三步运用了分解因式的 ;
A.提取公因式 B.逆用平方差公式 C.逆用完全平方公式
(2)该同学分解因式的结果不正确,应更正为 ;
(3)试分解因式n(n+1)(n+2)(n+3)+1.
【答案】
(1)C;(2)(x-2)4;(3)(n2+3n+1)2
【解析】
试题分析:(1)仔细分析式子的特征结合平方差公式、完全平方公式的特征分析即可;
(2)根据因式分解最终结果要分解彻底即可求得结果;
(3)先去括号,再根据多项式的特征解析分析即可,注意解本题要有整体意识.
(1)该同学第二步到第三步运用了分解因式的逆用完全平方公式;
(2)该同学分解因式的结果不正确,应更正为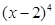 ;
;
(3)n(n+1)(n+2)(n+3)+1=n(n+3) (n+1)(n+2)+1=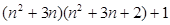
设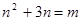 ,原式
,原式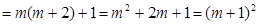
所以n(n+1)(n+2)(n+3)+1=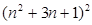 .
.
考点:公式法分解因式
点评:此类问题是初中数学的重点,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
相关题目
 进行因式分解的过程.
进行因式分解的过程.
 (第一步)
(第一步) (第二步)
(第二步) (第三步)
(第三步) (第四步)
(第四步) 进行因式分解.
进行因式分解.