题目内容
(1)如图1,△ABC中,AF平分∠BAC交BC于F,FD⊥AB于D,FE⊥AC于E,求证:AF垂直平分DE.
(2)如图2,分别以△ABC的边AB、AC为边向外作等边三角形ABD和等边三角形ACE,CD与BE相交于点O,判断∠AOD与∠AOE的数量关系,并证明;
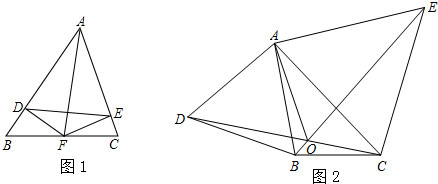
(2)如图2,分别以△ABC的边AB、AC为边向外作等边三角形ABD和等边三角形ACE,CD与BE相交于点O,判断∠AOD与∠AOE的数量关系,并证明;

分析:(1)根据角平分线上的点到角的两边的距离相等求出FD=FE,然后利用HL定理证明△ADF和△AEF全等,再根据全等三角形对应边相等得到AD=AE,最后利用等腰三角形“三线合一”的性质可得AF垂直平分DE;
(2)过点A作AM⊥DC于M,AN⊥BE于N,推出△DAC≌△BAE,可知它们的面积相等,即可推出AM=AN,即可推出:∠AOD=∠AOE.
(2)过点A作AM⊥DC于M,AN⊥BE于N,推出△DAC≌△BAE,可知它们的面积相等,即可推出AM=AN,即可推出:∠AOD=∠AOE.
解答:证明:(1)∵AF平分∠BAC交BC于F,FD⊥AB于D,FE⊥AC于E,
∴FD=FE(角平分线上的点到角的两边的距离相等),
在Rt△ADF和Rt△AEF中,
,
∴Rt△ADF≌Rt△AEF(HL),
∴AD=AE(全等三角形对应边相等),
又∵AF平分∠BAC交BC于F,
∴AF垂直平分DE(等腰三角形三线合一).
(2)∠AOD与∠AOE的数量关系为相等.
如图,过点A作AM⊥DC于M,AN⊥BE于N,
∵△ABD和△ACE都是等边三角形,
∴AD=AB,AC=AE,∠DAB=∠CAE=60°.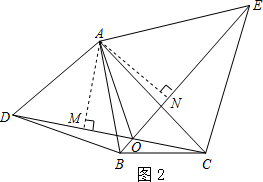
∴∠DAB+∠BAC=∠EAC+∠BAC,
即∠DAC=∠BAE,
在△DAC和△BAE中
,
∴△DAC≌△BAE(SAS).
∴DC=BE,
∴S△DAC=S△BAE.
∵S△DAC=
DC•AM=S△BAE=
BE•AN,
∴AM=AN.
∴点A在∠DOE的角平分线上.
∴∠AOD=∠AOE.
∴FD=FE(角平分线上的点到角的两边的距离相等),
在Rt△ADF和Rt△AEF中,
|
∴Rt△ADF≌Rt△AEF(HL),
∴AD=AE(全等三角形对应边相等),
又∵AF平分∠BAC交BC于F,
∴AF垂直平分DE(等腰三角形三线合一).
(2)∠AOD与∠AOE的数量关系为相等.
如图,过点A作AM⊥DC于M,AN⊥BE于N,
∵△ABD和△ACE都是等边三角形,
∴AD=AB,AC=AE,∠DAB=∠CAE=60°.

∴∠DAB+∠BAC=∠EAC+∠BAC,
即∠DAC=∠BAE,
在△DAC和△BAE中
|
∴△DAC≌△BAE(SAS).
∴DC=BE,
∴S△DAC=S△BAE.
∵S△DAC=
| 1 |
| 2 |
| 1 |
| 2 |
∴AM=AN.
∴点A在∠DOE的角平分线上.
∴∠AOD=∠AOE.
点评:本题主要考查全等三角形的判定和性质、角平分线的性质、等边三角形的性质,正确的作出辅助线是解决此题的关键.

练习册系列答案
相关题目
 如图,如果AB∥CD,那么下面说法错误的是( )
如图,如果AB∥CD,那么下面说法错误的是( ) 如图,直线AB、CD、MN相交于O,∠DOB=60°,BO⊥FO,OM平分∠DOF.
如图,直线AB、CD、MN相交于O,∠DOB=60°,BO⊥FO,OM平分∠DOF. 如图,直线AB、CD被直线CE所截.
如图,直线AB、CD被直线CE所截. 如图,直线AB、CD、EF相交于点O,∠COE=2∠AOE,已知∠BOC=105°,那么∠BOF=( )
如图,直线AB、CD、EF相交于点O,∠COE=2∠AOE,已知∠BOC=105°,那么∠BOF=( ) 如图,直线AB.CD相交于点O,OM⊥AB,NO⊥CD.
如图,直线AB.CD相交于点O,OM⊥AB,NO⊥CD.