题目内容
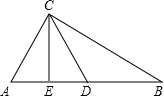 如图所示,在Rt△ABC中,CD是斜边上的中线,CE是高.已知AB=10cm,DE=2.5cm,则∠BDC=
如图所示,在Rt△ABC中,CD是斜边上的中线,CE是高.已知AB=10cm,DE=2.5cm,则∠BDC=120
120
度,S△BCD=25
| ||
| 4 |
25
| ||
| 4 |
分析:首先根据直角三角形斜边上的中线等于斜边的一半可得CD=5cm,再根据三角函数值算出∠ECD的度数,然后根据三角形的内角与外角的关系可得∠CDB=∠CED+∠ECD,进而得到∠CDB的度数;再根据勾股定理可计算出CE的长,然后再利用三角形的面积公式进行计算即可.
解答:解:∵在Rt△ABC中,CD是斜边上的中线,
∴CD=
AB,
∵AB=10cm,
∴CD=5cm,
∵CE是高,
∴△CED是直角三角形,
∵DE=2.5cm,
∴sin∠ECD=
=
,
∴∠ECD=30°,
∴∠CDB=∠CED+∠ECD=90°+30°=120°;
在Rt△CED中:CE=
=
=
(cm),
∴S△BCD=
DB•CE=
×5×
=
( cm2).
故答案为:120;
.
∴CD=
| 1 |
| 2 |
∵AB=10cm,

∴CD=5cm,
∵CE是高,
∴△CED是直角三角形,
∵DE=2.5cm,
∴sin∠ECD=
| DE |
| CD |
| 1 |
| 2 |
∴∠ECD=30°,
∴∠CDB=∠CED+∠ECD=90°+30°=120°;
在Rt△CED中:CE=
| CD2-ED2 |
| 52-2.52 |
5
| ||
| 2 |
∴S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
5
| ||
| 2 |
25
| ||
| 4 |
故答案为:120;
25
| ||
| 4 |
点评:此题主要考查了直角三角形的性质、勾股定理,以及三角函数的应用,解决问题的关键是掌握直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
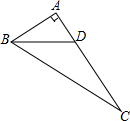 如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是( )
如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是( ) 21、如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB,∠A=55°,则∠DCB=
21、如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB,∠A=55°,则∠DCB= 22、如图所示,在Rt△ABC中,∠C=90°,∠A=30°.作AB的中垂线l分别交AB、AC及BC的延长线于点D、E、F,连接BE. 求证:EF=2DE.
22、如图所示,在Rt△ABC中,∠C=90°,∠A=30°.作AB的中垂线l分别交AB、AC及BC的延长线于点D、E、F,连接BE. 求证:EF=2DE. 如图所示,在Rt△ABC中,∠C=90°,AC=6,sinB=
如图所示,在Rt△ABC中,∠C=90°,AC=6,sinB= 如图所示,在Rt△ABC中,AD平分∠BAC,交BC于D,CH⊥AB于H,交AD于F,DE⊥AB垂足为E,求证:四边形CFED是菱形.
如图所示,在Rt△ABC中,AD平分∠BAC,交BC于D,CH⊥AB于H,交AD于F,DE⊥AB垂足为E,求证:四边形CFED是菱形.