题目内容
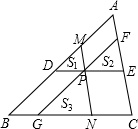 如图,DE∥BC,FG∥AB,MN∥AC,且DE、FG、MN交于点P.若记S△ABC=S,S△PDM=S1,S△PEF=S2,S△PGN=S3.请猜想:S与S1、S2、S3之间存在怎样的关系?你能加以验证吗?
如图,DE∥BC,FG∥AB,MN∥AC,且DE、FG、MN交于点P.若记S△ABC=S,S△PDM=S1,S△PEF=S2,S△PGN=S3.请猜想:S与S1、S2、S3之间存在怎样的关系?你能加以验证吗?
解:S与S1、S2、S3之间存在关系: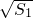 +
+ +
+ =
=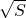 .
.
证明:∵FG∥AB,
∴△PDM∽△CBA,
∴ =
= ,
,
又∵DE∥BC,
∴四边形DPGB是平行四边形,
∴PD=BG,
∴ =
=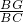 ,
,
同理: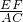 =
= ,
,
∴ +
+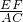 +
+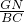 =
=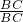 =1
=1
由△PDM∽△CBA得 =
=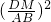 ,
,
即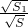 =
= ,
,
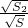 =
=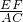 ,
,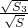 =
=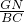 ,
,
∴即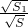 +
+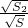 +
+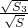 =1,
=1,
∴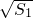 +
+ +
+ =
=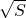 .
.
分析:根据DE∥BC,FG∥AB,MN∥AC,求证△PDM∽△CBA,利用四边形DPBG是平行四边形得出PD=BG, =
=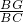 ,
,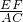 =
= ,进一步得出
,进一步得出 +
+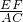 +
+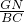 =
=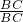 =1,再利用相似三角形面积比是相似比的平方即可得出结论.
=1,再利用相似三角形面积比是相似比的平方即可得出结论.
点评:此题主要考查学生对相似三角形的判定与性质,平行四边形的判定与性质,三角形面积的理解和掌握,利用相似三角形的相似比和平行四边形的性质得出 +
+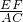 +
+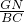 =
=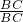 =1,这是此题的突破点,此题属于难题.
=1,这是此题的突破点,此题属于难题.
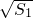 +
+ +
+ =
=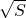 .
.证明:∵FG∥AB,
∴△PDM∽△CBA,
∴
 =
= ,
,又∵DE∥BC,
∴四边形DPGB是平行四边形,
∴PD=BG,
∴
 =
=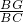 ,
,同理:
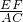 =
= ,
,∴
 +
+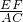 +
+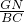 =
=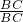 =1
=1由△PDM∽△CBA得
 =
=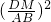 ,
,即
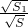 =
= ,
,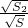 =
=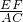 ,
,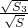 =
=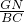 ,
,∴即
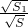 +
+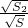 +
+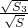 =1,
=1,∴
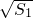 +
+ +
+ =
=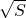 .
.分析:根据DE∥BC,FG∥AB,MN∥AC,求证△PDM∽△CBA,利用四边形DPBG是平行四边形得出PD=BG,
 =
=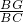 ,
,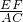 =
= ,进一步得出
,进一步得出 +
+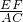 +
+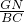 =
=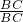 =1,再利用相似三角形面积比是相似比的平方即可得出结论.
=1,再利用相似三角形面积比是相似比的平方即可得出结论.点评:此题主要考查学生对相似三角形的判定与性质,平行四边形的判定与性质,三角形面积的理解和掌握,利用相似三角形的相似比和平行四边形的性质得出
 +
+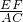 +
+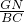 =
= =1,这是此题的突破点,此题属于难题.
=1,这是此题的突破点,此题属于难题. 
练习册系列答案
相关题目
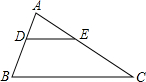 如图,DE∥BC,且DB=AE,若AB=5,AC=10,则AE的长为
如图,DE∥BC,且DB=AE,若AB=5,AC=10,则AE的长为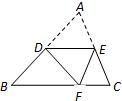 12、如图,DE∥BC,将△ABC沿DE所在的直线折叠,点A正好落在BC边上F处,若∠B=40°,则∠BDF=
12、如图,DE∥BC,将△ABC沿DE所在的直线折叠,点A正好落在BC边上F处,若∠B=40°,则∠BDF=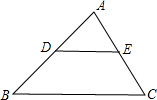 如图,DE∥BC,AD:DB=3:4,则△ADE与△ABC的周长之比为
如图,DE∥BC,AD:DB=3:4,则△ADE与△ABC的周长之比为 (1997•广西)如图,DE∥BC,AB=15,AC=9,BD=4,那么AE=( )
(1997•广西)如图,DE∥BC,AB=15,AC=9,BD=4,那么AE=( ) (1997•河北)已知:如图,DE∥BC,AD=3.6,DB=2.4,AC=7.求EC的长.
(1997•河北)已知:如图,DE∥BC,AD=3.6,DB=2.4,AC=7.求EC的长.