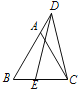题目内容
【题目】如图，边长为1的正△ABO的顶点O在原点，点B在x轴负半轴上，正方形OEDC边长为2，点C在y轴正半轴上，动点P从点A出发，以每秒1个单位的速度沿着△ABO的边按逆时针方向运动，动点Q从D点出发，以每秒1个单位的速度沿着正方形OEDC的边也按逆时针方向运动，点Q比点P迟1秒出发，则点P运动2016秒后，则PQ2的值是 ．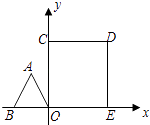 
【答案】8﹣
【解析】解：如图，作AH⊥DE于H，AN⊥BO于N，连接AM．
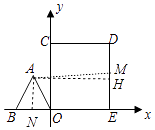
∵2016÷3=672，2016÷4=504，∵点Q比点P迟1秒出发，
∴运动2016秒后，点P在点A处，点Q在点M处（DM=ME=1），
∴PQ2=AM2=AH2+HM2
∵△ABC是等边三角形，AB=1，
∴AN= 
，NO= 
，
∵∠ANE=∠NEM=∠AME=90°，
∴四边形ANEM是矩形，
∴AH=NE，
∴AH= 
，HM=1﹣
∴PQ2=（ ）2+（1﹣ ）2=8﹣
所以答案是：8﹣
【考点精析】解答此题的关键在于理解正方形的性质的相关知识，掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．
【题目】如图，数轴上一动点
从原点出发，在数轴上进行往返运动，运动情况如下表（注：表格中的
表示2到4之间的数）.
运动次数 | 运动方向 | 运动路程 | 数轴上对应的数 |
第1次 | _________ | 3 | -3 |
第2次 | 左 |
| _________ |
第3次 | _________ | _________ |
|
回答下列问题：
（1）完成表格；
（2）已知第4次运动的路程为
.
①此时数轴上对应的数是_________；
②若第4次运动后点恰好回到原点，则这4次运动的总路程是多少？
