题目内容
【题目】小明在学习了如何证明“三边成比例的两个三角形相似”后,运用类似的思路证明了“两角分别相等的两个三角形相似”,以下是具体过程.
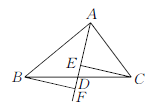
已知:如图,在△ABC和△![]() 中,∠A=∠
中,∠A=∠![]() ,∠B=∠
,∠B=∠![]() .
.
求证:△ABC∽△![]() .
.
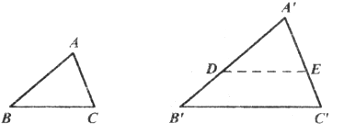
证明:在线段![]() 上截取
上截取![]() ,过点D作DE∥
,过点D作DE∥![]() ,交
,交![]() 于点E.
于点E.
由此得到△![]() ∽△
∽△![]() .
.
∴∠![]() =∠
=∠![]() ,
,
∵∠B=∠![]() ,
,
∴∠![]() =∠B,
=∠B,
∵∠![]() =∠A,
=∠A,
∴△![]() ≌△ABC,
≌△ABC,
∴△ABC∽△![]() .
.
小明将证明的基本思路概括如下,请补充完整:
(1)首先,通过作平行线,依据__________,可以判定所作△![]() 与_________;
与_________;
(2)然后,再依据相似三角形的对应角相等和已知条件可以证明所作△![]() 与________;
与________;
(3)最后,可证得△ABC∽△![]() .
.
【答案】(1)平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似;△![]() 相似;(2)△ABC全等.
相似;(2)△ABC全等.
【解析】
:在线段![]() 上截取
上截取![]() ,过点D作DE∥
,过点D作DE∥![]() ,交
,交![]() 于点E.由此得到△
于点E.由此得到△![]() ∽△
∽△![]() ,然后再证明△
,然后再证明△![]() ≌△ABC即可.
≌△ABC即可.
(1)首先,通过作平行线,依据平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似,可以判定所作△![]() 与△
与△![]() 相似;
相似;
(2)然后,再依据相似三角形的对应角相等和已知条件可以证明所作△![]() 与△ABC全等;
与△ABC全等;
(3)最后,可证得△ABC∽△![]() .
.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
【题目】近年来网约车十分流行,初三某班学生对“美团”和“滴滴”两家网约车公司各10名司机月收入进行了一项抽样调查,司机月收入(单位:千元)如图所示:

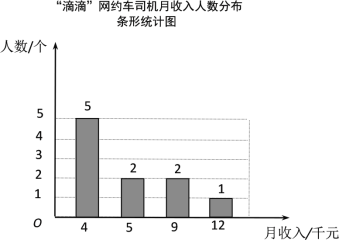
根据以上信息,整理分析数据如下:
平均月收入/千元 | 中位数/千元 | 众数/千元 | 方差/千元2 | |
“美团” | ① | 6 | 6 | 1.2 |
“滴滴” | 6 | ② | 4 | ③ |
(1)完成表格填空;
(2)若从两家公司中选择一家做网约车司机,你会选哪家公司,并说明理由.