题目内容
【题目】有一艘渔轮在海上C处作业时,发生故障,立即向搜救中心发出救援信号,此时搜救中心的两艘救助轮救助一号和救助二号分别位于海上A处和B处,B在A的正东方向,且相距100里,测得地点C在A的南偏东60,在B的南偏东30方向上,如图所示,若救助一号和救助二号的速度分别为40里/小时和30里/小时,问搜救中心应派那艘救助轮才能尽早赶到C处救援?(![]() ≈1.7)
≈1.7)

【答案】搜救中心应派2号艘救助轮才能尽早赶到C处救援
【解析】
作CD⊥AB交AB延长线于D,由等腰三角形的判定与性质求出BC的长,根据勾股定理分别计算出CD和AC的长度,利用速度、时间、路程之间的关系求出各自的时间比较大小即可.
解:作CD⊥AB交AB延长线于D,
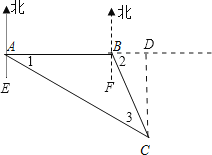
由已知得:∠EAC=60°,∠FBC=30°,
∴∠1=30°,∠2=90°-30°=60°,
∵∠1+∠3=∠2,
∴∠1=∠3,
∴AB=BC=100里,
在Rt△BDC中,BD=![]() BC=50里,
BC=50里,
∴CD=![]() 里,
里,
∵AD=AB+BD=150里,
∴在Rt△ACD中,AC=![]() 里,
里,
∵![]() ≈4.25小时,
≈4.25小时,![]() 小时,且
小时,且![]() <4.25,
<4.25,
∴搜救中心应派2号艘救助轮才能尽早赶到C处救援.

练习册系列答案
相关题目