题目内容
折叠矩形纸片ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm。

(1)求BF的长;(2)求折痕AE的长.

(1)求BF的长;(2)求折痕AE的长.
(1)BF=6cm;
(2)
(2)

试题分析:(1)因为点F为点D的折后的落点,所以△AFE≌△ADE,由此可得AF=AD=8,在△ABF中利用勾股定理,可得BF的值.
(2)只要求出DE的长,在△ADE中利用勾股定理可求的AE的长,设DE为x,则EF为x,在△CEF中利用勾股定理列方程,可求得DE的长.然后在RT△ADE中,由勾股定理可解得AE.
点评:此题要求掌握图形对折的问题,折叠前的图形与折叠后的图形全等,难度一般,熟练解直角三角形是解答本题的关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
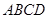 沿
沿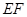 ,
,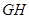 同时折叠,
同时折叠,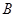 、
、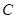 两点恰好都落在
两点恰好都落在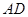 边的
边的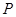 点处,若
点处,若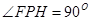 ,
,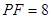 ,
,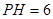 ,则长方形
,则长方形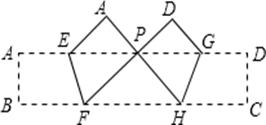

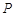 自B→A→E→B停止,点Q自D→F→C→D停止,点P运动的路程是m,点Q运动的路程是n,当四边形BPDQ是平行四边形时,求m与n满足的数量关系.(画出示意图)
自B→A→E→B停止,点Q自D→F→C→D停止,点P运动的路程是m,点Q运动的路程是n,当四边形BPDQ是平行四边形时,求m与n满足的数量关系.(画出示意图)
 ABCD的一边长为10,则对角线AC、BD的长可取下列数据中的( )
ABCD的一边长为10,则对角线AC、BD的长可取下列数据中的( )