题目内容
【题目】如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的.其中测得坡长AB=600米,BC=200米,坡角∠BAF=30°,∠CBE=45°.(结果保留根号)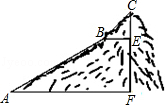
【答案】解:如图所示,过B作BG⊥AF于G,
则BG=EF、BE=GF,
∵AB=600,∠BAF=30°,
∴EF=BG= ![]() AB=300米,
AB=300米,
在Rt△BCE中,∵BC=200米,∠CBE=45°,
∴CE=BCsin∠CBE=200× ![]() =100
=100 ![]() (米),
(米),
∴CF=300+100 ![]() (米)
(米)
∴山峰的高度是(300+100 ![]() )米.
)米.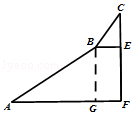
【解析】作BG⊥AF于G,在Rt△ABG中根据∠BAF=30°得出BG的长,从而得到EF的长,再在Rt△CBE中利用∠CBE的正弦计算出CE,然后计算CE和EF的和即可.

练习册系列答案
相关题目


