题目内容
【题目】甲骑自行车、乙骑摩托车沿相同路线由A地到B地，行驶过程中路程与时间的函数关系的图象如图. 根据图象解决下列问题：
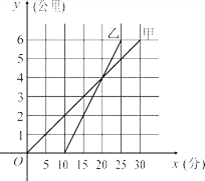
(1) 谁先出发？先出发多少时间？谁先到达终点？先到多少时间？
(2) 分别求出甲、乙两人的行驶速度；
(3) 在什么时间段内，两人均行驶在途中(不包括起点和终点)？在这一时间段内，请你根据下列情形，分别列出关于行驶时间x的方程或不等式(不化简，也不求解)：① 甲在乙的前面；② 甲与乙相遇；③ 甲在乙后面.
【答案】（1）甲先出发，先出发10分钟，乙先到达，先到达5分钟；（2）甲的速度为0.2（千米／分），乙的速度为0.4（千米／分）；（3）①甲在乙的前面：
；②甲与乙相遇：
，③甲在乙的后面：
．
【解析】
试题（1）因为当y=0时，
=0，
=10，所以甲先出发了10分钟，又因当y=6时，=30，=25，所以乙先到达了5分钟；
（2）都走了6公里，甲用了30分钟，乙用了25﹣10=15分钟，由此即可求出各自的速度；
（3）由图象，可知当10＜x＜25分钟时两人均行驶在途中，在图象中找出两图象上的点，利用待定系数法分别求出它们的解析式，然后即可列出不等式．
试题解析：（1）甲先出发，先出发10分钟．乙先到达终点，先到达5分钟；
（2）甲的速度为6÷30=0.2（千米／分），乙的速度为6÷（25―10）=0.4（千米／分）；
（3）当10＜x＜25分钟时两人均行驶在途中．设
=kx，因为=kx经过（30，6），所以6=30k，故k=0.2，∴=0.2x．设
=mx+b，∵=mx+b经过（10，0），（25，6），∴
，∴
，所以=
，
①当
时，即，10＜x＜20时，甲在乙的前面；
②当
时，即，x=20时，甲与乙相遇；
③当
时，即，20＜x＜25时，乙在甲的前面．
考前必练系列答案
【题目】某校为了了解学生大课间活动的跳绳情况，随机抽取了50名学生每分钟跳绳的次数进行统计，把统计结果绘制成如表和直方图．
次数 | 70≤x＜90 | 90≤x＜110 | 110≤x＜130 | 130≤x＜150 | 150≤x＜170 |
人数 | 8 | 23 | 16 | 2 | 1 |
根据所给信息，回答下列问题：
（1）本次调查的样本容量是；
（2）本次调查中每分钟跳绳次数达到110次以上（含110次）的共有的共有人；
（3）根据上表的数据补全直方图；
（4）如果跳绳次数达到130次以上的3人中有2名女生和一名男生，学校从这3人中抽取2名学生进行经验交流，求恰好抽中一男一女的概率（要求用列表法或树状图写出分析过程）．
