题目内容
【题目】已知,在四边形ABCD中,点E、点F分别为AD、BC的中点,连接EF.
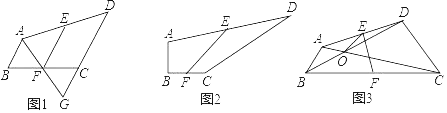
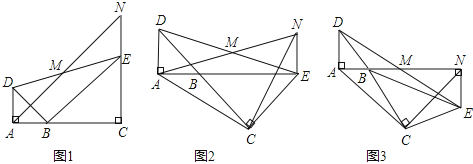
(1)如图1,AB∥CD,连接AF并延长交DC的延长线于点G,则AB、CD、EF之间的数量关系为 ;
(2)如图2,∠B=90°,∠C=150°,求AB、CD、EF之间的数量关系?
(3)如图3,∠ABC=∠BCD=45°,连接AC、BD交于点O,连接OE,若AB=![]() ,CD=2
,CD=2![]() ,BC=6,则OE= .
,BC=6,则OE= .
【答案】(1)AB+CD=2EF;(2)4EF2=AB2+CD2+ABCD,证明详见解析;(3)![]() .
.
【解析】
(1)根据三角形的中位线和全等三角形的判定和性质解答即可;
(2)如图2中,作CK⊥BC,连接AF,延长AF交CK于K.连接DK,作DH⊥CK于H.首先证明△AFB≌△KFC,推出AB=CK,再利用勾股定理,三角形的中位线定理即可解决问题;
(3)如图3中,以点B为原点,BC为x轴,建立平面直角坐标系如图所示.想办法求出点E、O的坐标即可解决问题;
解:(1)结论:AB+CD=2EF,
理由:如图1中,
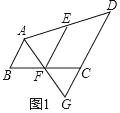
∵点E、点F分别为AD、BC的中点,
∴BF=FC,AE=ED,
∵AB∥CD,
∴∠ABF=∠GCF,
∵∠BFA=∠CFG,
∴△ABF≌△GCF(ASA),
∴AB=CG,AF=FG,
∵AE=ED,AF=FG,
∴2EF=DG=DC+CG=DC+AB;
∴AB+CD=2EF;
(2)如图2中,作CK⊥BC,连接AF,延长AF交CK于K.连接DK,作DH⊥CK于H.
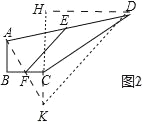
∵∠ABF=∠KCF,BF=FC,∠AFB=∠CFK,
∴△AFB≌△KFC,
∴AB=CK,AF=FK,
∵∠BCD=150°,∠BCK=90°,
∴∠DCK=120°,
∴∠DCH=60°,
∴CH=![]() CD,DH=
CD,DH=![]() CD,
CD,
在Rt△DKH中,DK2=DH2+KH2=(![]() CD)2+(AB+
CD)2+(AB+![]() CD)2=AB2+CD2+ABCD,
CD)2=AB2+CD2+ABCD,
∵AE=ED,AF=FK,
∴EF=![]() DK,
DK,
∴4EF2=DK2,
∴4EF2=AB2+CD2+ABCD.
(3)如图3中,以点B为原点,BC为x轴,建立平面直角坐标系如图所示.
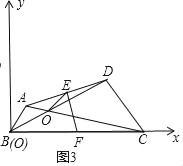
由题意:A(1,1),B(0,0),D(4,2),
∵AE=ED,
∴![]() ,
,![]() ),
),
∵AC的解析式为y=-![]() x+
x+![]() ,BD的解析式为y=
,BD的解析式为y=![]() x,
x,
由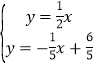 ,解得
,解得 ,
,
∴O(![]() ,
,![]() ),
),
∴OE=![]() =
=![]() .
.
故答案为:(1)AB+CD=2EF;(2)4EF2=AB2+CD2+ABCD,证明详见解析;(3)![]() .
.