题目内容
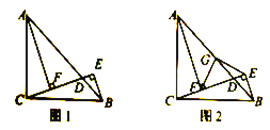
【题目】如图,CE是平行四边形ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E,连接AC,BE,则下列结论:①AC=AD;②AO=![]() ;③四边形ACBE是菱形;④
;③四边形ACBE是菱形;④![]() .其中正确的结论有____.(填写所有正确结论的序号)
.其中正确的结论有____.(填写所有正确结论的序号)

【答案】①②③④;
【解析】
根据平行四边形的性质以及判定定理、菱形的判定方法、平行线分线段成比例定理一一判断即可;
解:解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD(平行四边形对边相等且平行),
∵EC垂直平分AB,
∴![]() ,故②正确,
,故②正确,
∴![]() ,
,
∵OA∥DC,
![]() ,
,
∴AE=AD,OE=OC,
∵OA=OB,OE=OC,
∴四边形ACBE是平行四边形(对角线相互平分的四边形是平行四边形),
∵AB⊥EC,
∴四边形ACBE是菱形(对角线相互垂直的四边形是菱形),故③正确,
∵∠DCE=90°,DA=AE,
∴AC=AD=AE,故①正确;
∵![]() ,
,
![]() ,
,
∴![]() ,故④正确;
,故④正确;
综上①②③④均正确,
故答案为:①②③④;

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目