题目内容
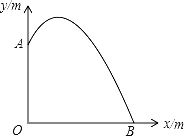
【题目】学校与图书馆在同一条笔直道路上。甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地。两人之间的距离![]() (米)与时间
(米)与时间![]() (分钟)之间的函数关系如图所示。
(分钟)之间的函数关系如图所示。
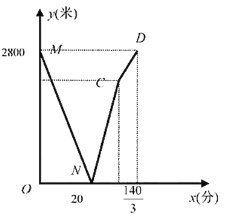
(1)当![]() ____________分钟时甲、乙两人相遇,乙的速度为__________米/分钟,点
____________分钟时甲、乙两人相遇,乙的速度为__________米/分钟,点![]() 的坐标为_____________;
的坐标为_____________;
(2)求出甲、乙两人相遇后![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)当乙到达距学校800米处时,求甲、乙两人之间的距离。
【答案】(1)20,80,![]() ;(2)
;(2)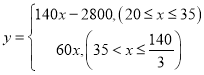 ;(3)甲、乙两人之间的距离为700米.
;(3)甲、乙两人之间的距离为700米.
【解析】
(1)由图象知:当y=0时对应的x的值即为甲、乙两人相遇的时间;甲用了![]() 分钟走了2800米,所以可求甲的速度,再根据甲乙两人速度和是
分钟走了2800米,所以可求甲的速度,再根据甲乙两人速度和是![]() 米/分钟可求出乙的速度;用乙的总路程2800米除以乙的速度即为乙从图书馆回学校的时间,即为点C的横坐标,用点C的横坐标乘以甲的速度即可得出点C的纵坐标;
米/分钟可求出乙的速度;用乙的总路程2800米除以乙的速度即为乙从图书馆回学校的时间,即为点C的横坐标,用点C的横坐标乘以甲的速度即可得出点C的纵坐标;
(2)分NC段和CD段两种情况利用待定系数法求解即可;
(3)先求出乙到达距学校800米处时所用的时间,再用甲乙两人的速度和乘以这个时间减去2800米即为所求.
解:(1)当x=24分钟时,甲、乙两人相遇;
由图象知:甲用了![]() 分钟走了2800米,所以甲的速度为:
分钟走了2800米,所以甲的速度为:![]() 米/分钟,甲乙两人的速度和为:
米/分钟,甲乙两人的速度和为:![]() 米/分钟,所以乙的速度是:140-60=80米/分钟;
米/分钟,所以乙的速度是:140-60=80米/分钟;
乙从图书馆回学校的时间是:2800÷80=35分钟,35×60=2100,所以点C的坐标是![]() .
.
故答案为:20,80,![]() ;
;
(2)设![]() 段所求函数关系式为
段所求函数关系式为![]() ,
,
则![]() ,解得
,解得![]() ,
,
∴![]() ;
;
设![]() 段所求函数关系式为
段所求函数关系式为![]() ,
,
则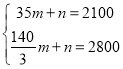 ,解得
,解得![]() ,
,
∴![]() ,
,
综上: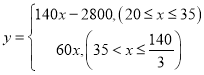 ;
;
(3)![]() (分钟),
(分钟),
当![]() 时,
时,![]() (米),
(米),
答:甲、乙两人之间的距离为700米.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目