题目内容
【题目】如图1,已知正方形ABCD和正方形AEFG有公共顶点A,连接BE,DG.


(1)问:BE与DG有什么关系?说明理由.
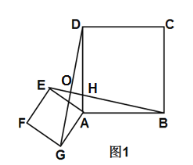
(2)如图2,已知AB=4,AE=![]() ,当点F在边AD上时,求BE的长.
,当点F在边AD上时,求BE的长.
【答案】(1)BE=DG且BE⊥DG;理由见解析;(2)BE=![]() .
.
【解析】
(1)设BE和DG相交于点O,AD和BE相交于点H,根据正方形的性质,可得AD=AB,AG=AE,∠DAB=∠EAG=90,利用SAS证明△EAB≌△GAD,得出BE=DG,∠GDA=∠EBA,推出∠DOH=∠HAB=90,即可求得.
(2)过点E作EM,已知四边形AEFG是正方形,四边形ABCD是正方形,∠EAF=∠FAG=45,∠DAB=90,可得∠EAM=45,已知AE,即可求得AM,BM,利用勾股定理即可求出BE.
(1)设BE和DG相交于点O,AD和BE相交于点H
∵四边形ABCD是正方形
∴AD=AB,∠DAB=90
∵四边形AEFG是正方形
∴AG=AE,∠EAG=90
∴∠EAB=∠EAD+∠DAB=∠EAD+∠EAG=∠GAD
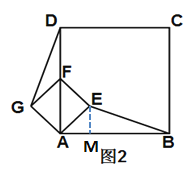
∴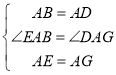
∴△EAB≌△GAD
∴BE=DG,∠GDA=∠EBA
∵∠DHO=∠BHA
∴∠DOH=∠HAB==90
∴BE⊥DG
故答案为:BE=DG且BE⊥DG
(2)过点E作EM
∵四边形AEFG是正方形
∴∠EAF=∠FAG=45
∵∵四边形ABCD是正方形
∴∠DAB=90
∴∠EAM=45
∴AM=EM
∵![]()
∴![]()
∴AM=1
∴MB=AB-AM=4-1=3
∴![]()
故答案为:![]()

练习册系列答案
相关题目






