题目内容
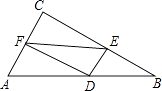
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于N,连接MN,DN.请你判定四边形BMDN是什么特殊四边形,并说明理由. 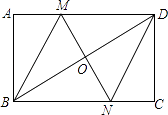
【答案】解:四边形BMDN是菱形.理由如下: ∵四边形ABCD是矩形,
∴AD∥BC,OD=OB,
∴∠MDO=∠NBO,
∵MN是BD的垂直平分线
∴在△MOD与△NOB中,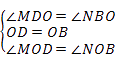 ,
,
∴△MOD≌△NOB(ASA),
∴MO=NO,
∴四边形BMDN是平行四边形.
∵MN是BD的垂直平分线,
∴平行四边形BMDN是菱形.
【解析】根据全等三角形的判定定理ASA证得△MOD≌△NOB,则由全等三角形的对应边相等推知MO=NO,所以“对角线互相平分的四边形BMDN是平行四边形,然后由”对角线互相垂直平分的平行四边形是菱形“证得结论﹣﹣四边形BMDN是菱形. ∴∠MOD=∠NOB=90°.
【考点精析】根据题目的已知条件,利用菱形的判定方法和矩形的性质的相关知识可以得到问题的答案,需要掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形;矩形的四个角都是直角,矩形的对角线相等.

练习册系列答案
相关题目