题目内容
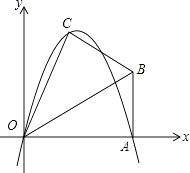
【题目】如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y= ![]() (x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )
(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )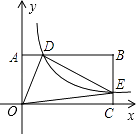
A.![]()
B.![]()
C.![]()
D.12
【答案】C
【解析】解:∵四边形OCBA是矩形,
∴AB=OC,OA=BC,
设B点的坐标为(a,b),
∵BD=3AD,
∴D( ![]() ,b),
,b),
∵点D,E在反比例函数的图象上,
∴ ![]() =k,∴E(a,
=k,∴E(a, ![]() ),
),
∵S△ODE=S矩形OCBA﹣S△AOD﹣S△OCE﹣S△BDE=ab﹣ ![]()
![]() ﹣
﹣ ![]()
![]() ﹣
﹣ ![]()
![]() (b﹣
(b﹣ ![]() )=9,
)=9,
∴k= ![]() ,
,
所以答案是:C.
【考点精析】解答此题的关键在于理解反比例函数的性质的相关知识,掌握性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大,以及对三角形的面积的理解,了解三角形的面积=1/2×底×高.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目