题目内容
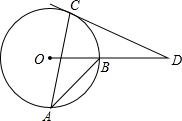如图，AB、AC是⊙O的两条弦∠A=25°，过点C的切线与OB的延长线交于点D，则∠D的度数是40°
40°
．分析：由于CD是切线，可知∠OCD=90°，而∠A=25°，利用圆周角定理可求∠COD，进而可求∠D．
解答：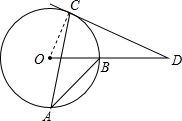
解：连接OC，
∵CD是切线，
∴∠OCD=90°，
∵∠A=25°，
∴∠COD=2∠A=50°，
∴∠D=90°-50°=40°．
故答案为40°．
解：连接OC，∵CD是切线，
∴∠OCD=90°，
∵∠A=25°，
∴∠COD=2∠A=50°，
∴∠D=90°-50°=40°．
故答案为40°．
点评：本题利用了切线的概念和圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
D交OB的延长线于点D．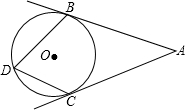
如图，AB、AC是⊙O的切线，且∠A=54°，则∠BDC=
如图，AB，AC是圆的两条弦，AD是圆的一条直径，且BC⊥AD，下列结论中不一定正确的是（ ）
如图，AB和AC是等腰△ABC的两腰，CD和BE是两腰上的高，CD和BE相交于点F．