题目内容
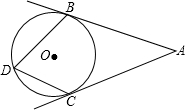 如图,AB、AC是⊙O的两条切线,切点分别为B、C,D是优弧
如图,AB、AC是⊙O的两条切线,切点分别为B、C,D是优弧 | BC |
50
50
度.(直接写答案)分析:连接OB,OC,由AB与AC为圆O的切线,根据切线的性质得到AB垂直于OB,AC垂直于OC,在四边形ABOC中,由∠BAC的度数,以及两个角为直角,利用四边形的内角和定理求出∠BOC的度数,再利用同弧所对的圆周角等于所对圆心角的一半,可得出所求角的度数.
解答:解:连接OB,OC,如图所示:
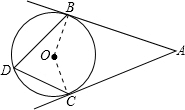
∵AB,AC分别为圆O的切线,
∴AB⊥OB,AC⊥OC,
∴∠ABO=∠ACO=90°,又∠BAC=80°,
∴∠BOC=360°-(∠ABO-∠ACO-∠BAC)=100°,
又圆心角∠BOC与圆周角∠BDC都对弧
,
∴∠BDC=
∠BOC=50°.
故答案为:50

∵AB,AC分别为圆O的切线,
∴AB⊥OB,AC⊥OC,
∴∠ABO=∠ACO=90°,又∠BAC=80°,
∴∠BOC=360°-(∠ABO-∠ACO-∠BAC)=100°,
又圆心角∠BOC与圆周角∠BDC都对弧
 |
| BC |
∴∠BDC=
| 1 |
| 2 |
故答案为:50
点评:此题考查了切线的性质,四边形的内角和定理,以及圆周角定理,遇到切线,常常连接圆心与切点,根据切线性质构造直角三角形来解决问题,熟练掌握切线的性质是解本题的关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 D交OB的延长线于点D.
D交OB的延长线于点D. 如图,AB,AC是圆的两条弦,AD是圆的一条直径,且BC⊥AD,下列结论中不一定正确的是( )
如图,AB,AC是圆的两条弦,AD是圆的一条直径,且BC⊥AD,下列结论中不一定正确的是( ) 如图,AB和AC是等腰△ABC的两腰,CD和BE是两腰上的高,CD和BE相交于点F.
如图,AB和AC是等腰△ABC的两腰,CD和BE是两腰上的高,CD和BE相交于点F.