题目内容
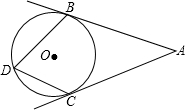如图，AB、AC是⊙O的切线，且∠A=54°，则∠BDC=分析：连接OB、OC，根据四边形的内角和求得∠BOC，再由圆周角定理得出∠D．
解答：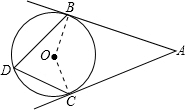
解：连接OB、OC，
∵AB、AC是⊙O的切线，
∴∠OBA=∠OCA=90°，
∵∠A=54°，
∴∠BOC=126°，
∴∠BDC=
∠BOC=63°．
故答案为：63°．
解：连接OB、OC，∵AB、AC是⊙O的切线，
∴∠OBA=∠OCA=90°，
∵∠A=54°，
∴∠BOC=126°，
∴∠BDC=
| 1 |
| 2 |
故答案为：63°．
点评：本题考查了切线长定理、圆周角定理和四边形的内角和，是基础知识要熟练掌握．
练习册系列答案
相关题目
D交OB的延长线于点D．
如图，AB，AC是圆的两条弦，AD是圆的一条直径，且BC⊥AD，下列结论中不一定正确的是（ ）
如图，AB和AC是等腰△ABC的两腰，CD和BE是两腰上的高，CD和BE相交于点F．