题目内容
如图,AB,AC是⊙O的两条切线,切点分别为B,C,连接OB,OC,在⊙O外作∠BAD=∠BAO,A D交OB的延长线于点D.
D交OB的延长线于点D.(1)在图中找出一对全等三角形,并进行证明;
(2)如果⊙O的半径为3,sin∠OAC=
| 1 | 2 |
(3)试说明:△ABD分别是由△ABO,△ACO经过哪种变换得到的.(直接写出结果)
分析:本题可根据三角形全等,切线的性质,图形的旋转解答.
(1)直接利用全等的条件易证△ACO≌△ABO;
(2)利用切线的性质可得到直角三角形,利用三角函数值可分别求得所需线段的长度,再利用勾股定理求得AC的长;
(3)利用旋转的性质和轴对称的性质可直接得到.
(1)直接利用全等的条件易证△ACO≌△ABO;
(2)利用切线的性质可得到直角三角形,利用三角函数值可分别求得所需线段的长度,再利用勾股定理求得AC的长;
(3)利用旋转的性质和轴对称的性质可直接得到.
解答:解:(1)在△ACO与△ABO中,
∵OC=OB,∠ABO=∠ACO=90°,
∴∠BAO=∠CAO,OA为公共边.
∴△ACO≌△ABO.
(2)∵AC切⊙O于点C,
∴OC⊥AC;
在Rt△ACO中,
∵sin∠OAC=
,
∴
=
.
∵OC=3,
∴AO=6.
∴AC=
=
=3
.
(3)△ABD是由△ABO沿直线AB折叠得到(或△ABD与△ABO关于直线AB对称),
△ABD是由△ACO绕A点顺时针方向旋转∠CAB(或∠OAD)而得到.
∵OC=OB,∠ABO=∠ACO=90°,
∴∠BAO=∠CAO,OA为公共边.
∴△ACO≌△ABO.
(2)∵AC切⊙O于点C,
∴OC⊥AC;
在Rt△ACO中,
∵sin∠OAC=
| 1 |
| 2 |
∴
| OC |
| OA |
| 1 |
| 2 |
∵OC=3,
∴AO=6.
∴AC=
| AO2-OC2 |
| 62-32 |
| 3 |
(3)△ABD是由△ABO沿直线AB折叠得到(或△ABD与△ABO关于直线AB对称),
△ABD是由△ACO绕A点顺时针方向旋转∠CAB(或∠OAD)而得到.
点评:本题的信息量较大,涉及面较广,是一道较有难度的题目,同学们需细心解答.

练习册系列答案
相关题目
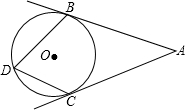 如图,AB、AC是⊙O的切线,且∠A=54°,则∠BDC=
如图,AB、AC是⊙O的切线,且∠A=54°,则∠BDC=
 如图,AB,AC是圆的两条弦,AD是圆的一条直径,且BC⊥AD,下列结论中不一定正确的是( )
如图,AB,AC是圆的两条弦,AD是圆的一条直径,且BC⊥AD,下列结论中不一定正确的是( ) 如图,AB和AC是等腰△ABC的两腰,CD和BE是两腰上的高,CD和BE相交于点F.
如图,AB和AC是等腰△ABC的两腰,CD和BE是两腰上的高,CD和BE相交于点F.