题目内容
【题目】如图,四边形ABCD中,AD∥BC,∠B=90°,E为AB的中点,分别以ED,EC为折痕将两个角,(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处,若AD=4,BC=9,则EF的值是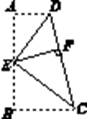
【答案】6
【解析】如图,由翻折变换的性质得:
DF=DA=4,CF=CB=6;
∠DEA=∠DEF,∠CEF=∠CEB,
![]() 由射影定理得:
由射影定理得: ![]()
∴EF=6,
所以答案是:6.
【考点精析】本题主要考查了翻折变换(折叠问题)和相似三角形的判定与性质的相关知识点,需要掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.

练习册系列答案
相关题目