题目内容
【题目】(问题背景)
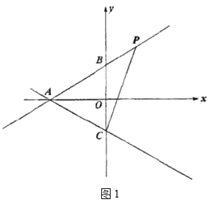
(1)如图1的图形我们把它称为“8字形”,请说理证明∠A+∠B=∠C+∠D
![]()


(简单应用)
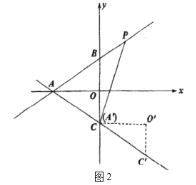
(2)如图2,AP、CP分别平分∠BAD、∠BCD,若∠ABC=20°,∠ADC=26°,求∠P的度数(可直接使用问题(1)中的结论)
(问题探究)
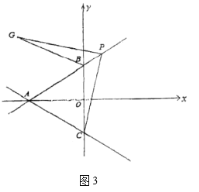
(3)如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,试求∠P的度数
【答案】(1)见解析;(2)23°;(3)26°
【解析】
(1)根据三角形内角和定理即可证明;
(2)如图2,根据角平分线的性质得到∠1=∠2,∠3=∠4,列方程组即可得到结论;
(3)由AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,推出∠1=∠2,∠3=∠4,推出∠PAD=180°-∠2,∠PCD=180°-∠3,由∠P+(180°-∠1)=∠D+(180°-∠3),∠P+∠1=∠B+∠4,推出2∠P=∠B+∠D,即可解决问题
(1)证明:在△AOB中,∠A+∠B+∠AOB=180°,
在△COD中,∠C+∠D+∠COD=180°,
∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D;
(2)解:如图2,∵AP、CP分别平分∠BAD,∠BCD,
∴∠1=∠2,∠3=∠4,
由(1)的结论得: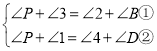 ,
,
①+②,得2∠P+∠1+∠3=∠2+∠4+∠B+∠D,
∴∠P=![]() (∠B+∠D)=23°;
(∠B+∠D)=23°;
(3)解:如图3,
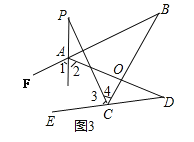
∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠1=∠2,∠3=∠4,
∴∠PAD=180°﹣∠2,∠PCD=180°﹣∠3,
∵∠P+(180°﹣∠2)=∠D+(180°﹣∠3),
∵∠P+∠1=∠B+∠4,
∴2∠P=∠B+∠D,
∴∠P=![]() (∠B+∠D)=
(∠B+∠D)=![]() ×(36°+16°)=26°.
×(36°+16°)=26°.
故答案为:(1)见解析;(2)23°;(3)26°.

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案【题目】某服装店用6000元购进A,B两种新式服装,按标价售出后可获得毛利润3800元(毛利润=售价﹣进价),这两种服装的进价、标价如下表所示:
类型 价格 | A型 | B型 |
进价(元/件) | 60 | 100 |
标价(元/件) | 100 | 160 |
(1)求这两种服装各购进的件数;
(2)如果A中服装按标价的8折出售,B中服装按标价的7折出售,那么这批服装全部售完后,服装店比按标价售出少收入多少元?
【题目】某公司有A、B两种型号的客车共11辆,它们的载客量(不含司机)、日租金、车辆数如下表所示,已知这11辆客车满载时可搭载乘客350人.
A型客车 | B型客车 | |
载客量(人/辆) | 40 | 25 |
日租金(元/辆) | 320 | 200 |
车辆数(辆) | a | b |
(1)求a、b的值;
(2)某校七年级师生周日集体参加社会实践,计划租用A、B两种型号的客车共6辆,且租车总费用不超过1700元.
①最多能租用A型客车多少辆?
②若七年级师生共195人,写出所有的租车方案,并确定最省钱的租车方案.