题目内容
如图,□ABCD中,点E在AB边上,将△EBC沿CE所在直线折叠,使点B落在AD边上的点B′处,再将折叠后的图形打开,若△AB′E的周长为4cm,△B′DC的周长为11cm,则B′D的长为_________cm.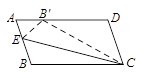

3.5
试题考查知识点:轴对称图形的性质;平行四边形的性质。
思路分析:利用对称特点求出平行四边形的周长,再通过平行四边形各部分的重新组合,从而推导出所要求线段长。
具体解答过程:
∵四边形ABCD是平行四边形,
∴AB=DC,AD=BC
△EBC沿CE所在直线折叠,使点B落在AD边上的点B′处,
∴△BEC与△B′EC关于CE所在直线对称,EB′=EB,BC=B′C
∵△AB′E的周长为L1=4cm,△B′DC的周长为L2=11cm
∴□ABCD的周长为L=L1+L2=4cm+11cm=15cm,CD+BC=
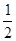 L=
L=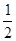 ×15=7.5cm
×15=7.5cm∴B′D=L-CD-BC-AB-AB′=L-(CD+BC)-(AE+EB+AB′)=L-(CD+BC)-L1=15-7.5-4=3.5cm
试题点评:替代法(等量代换)在几何题目中,是常用的方法。

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目

 .
.
 ;
; ,求
,求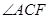 的度数.
的度数.
 和2
和2


