题目内容
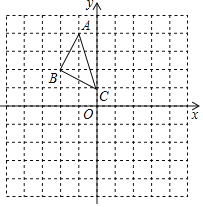
【题目】△ABC在平面直角坐标系中的位置如图所示，将△ABC沿y轴翻折得到△A1B1C1，再将△A1B1C1绕点O旋转180°得到△A2B2C2；已知A（﹣1，4），B（﹣2，2），C（0，1）
（1）请依次画出△A1B1C1和△A2B2C2；
（2）若直线A1B2与一个反比例函数图象在第一象限交于点A1，试求直线A1B2和这个反比例函数的解析式．
【答案】（1）详见解析；（2）y＝
，y＝2x+2．
【解析】
（1）根据网格结构找出点A、B、C关于y轴的对称点A1、B1、C1的位置，然后顺次连接即可；再找出点A1、B1、C1绕点O旋转180°后的对应点A2、B2、C2的位置，然后顺次连接即可；
（2）由于A、A1关于y轴对称，那么它们的横坐标互为相反数，纵坐标相同，由此得A1的坐标，由于B1、B2关于原点对称，那么它们的横纵坐标互为相反数，由此得B2的坐标，然后根据待定系数法求得直线A1B2和这个反比例函数的解析式．
解：（1）△A1B1C1和△A2B2C2如图所示；
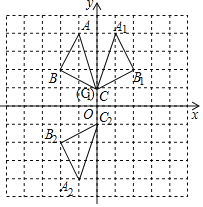
（2）由题意可知A1（1，4），B1（2，2），
∴B2（﹣2，﹣2），
设反比例函数的解析式为y＝
，直线A1B2的解析式为y＝ax+b，
∵反比例函数图象经过点A1，
∴k＝1×4＝4，
∴反比例函数的解析式为y＝，
把A1（1，4），B2（﹣2，﹣2）代入y＝ax+b得
，
解得
，
∴直线A1B2的解析式为y＝2x+2．
练习册系列答案
相关题目
