题目内容
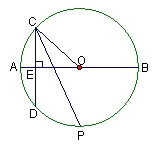
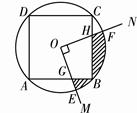
如图所示，四边形ABCD中，DC∥AB，BC=1，AB=AC=AD=2．则BD的长为（ ）
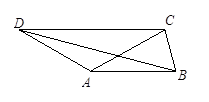
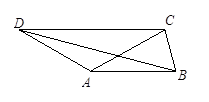
A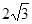． | B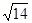． | C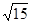． | D． |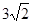
C
解：以A为圆心，AB长为半径作圆，延长BA交⊙A于F，连接DF．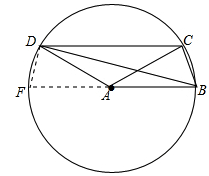
∵AB=AC=AD=2，
∴D，C在圆A上，
∵DC∥AB，
∴弧DF=弧BC，
∴DF=CB=1，BF=AB+AF=2AB=4，
∵FB是⊙A的直径，
∴∠FDB=90°，
∴BD=
= 
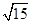
故选C
∵AB=AC=AD=2，
∴D，C在圆A上，
∵DC∥AB，
∴弧DF=弧BC，
∴DF=CB=1，BF=AB+AF=2AB=4，
∵FB是⊙A的直径，
∴∠FDB=90°，
∴BD=
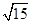
= 故选C
练习册系列答案
相关题目
．
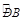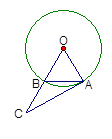
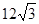cm，点B在y轴的正半轴上，OB=12cm，动点P从点A开始沿AO以
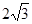cm/s的速度向点O移动，移动时间为t s(0＜t＜6).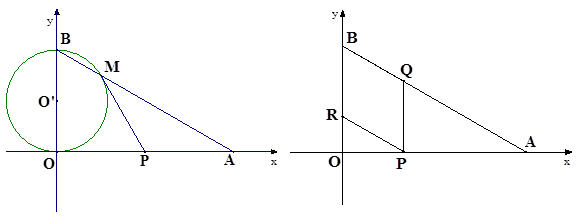
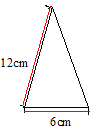
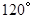的扇形围成一个圆锥的侧面（接缝忽略不计），则这个圆锥的底面半径是 。
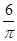cm，母线长为15cm，已知在加工灯罩的过程中，材料损耗率为10%，那么加工100个这样的灯罩，实际需要的铁皮面积为（不计接缝） cm2。