题目内容
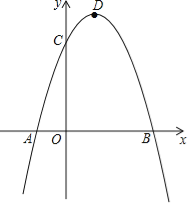
【题目】抛物线y=ax2+bx+c(a>0)经过点A(-3![]() ,0)、B(
,0)、B(![]() ,0),它与y轴相交于点C,且∠ACB≥90°,设该抛物线的顶点为D,△BCD的边CD上的高为h.
,0),它与y轴相交于点C,且∠ACB≥90°,设该抛物线的顶点为D,△BCD的边CD上的高为h.
(1)求实数a的取值范围;
(2)求高h的取值范围;
(3)当(1)的实数a取得最大值时,求此时△BCD外接圆的半径.
【答案】(1)0<a≤![]() ;(2)0<h≤
;(2)0<h≤![]() ;(3)2
;(3)2![]() .
.
【解析】
(1)利用直角三角形各边的关系,求得OC2=OAOB,利用边角关系,代入a值解得.
(2)过D作DE⊥OC,延长DC交x轴于点H,过点B作BF⊥CH于点F.利用顶点公式求得点D,由OC≤3,则tan∠OHC=![]() ≤
≤![]() ,从而解得.
,从而解得.
(3)求得a的最大值,求得h值,可得BD,BC,连接DG,由△DGB∽△BCF求得DG.
解:(1)当∠ACB=90°时,OC2=OAOB,
得OC=3
又∠ACB≥90°,
故OC≤3,
所以9a≤3,
∴0<a≤![]() .
.
(2)过D作DE⊥OC,延长DC交x轴于点H,过点B作BF⊥CH于点F.
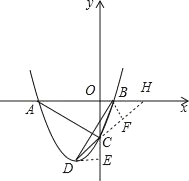
因为D为抛物线的顶点,
所以D(-![]() ,﹣12a),OE=12a,
,﹣12a),OE=12a,
又∵OC=9a,CE=3a,DE=![]() ,
,
易证△HCO∽△DCE,
有![]() =3,
=3,
故OH=3DE=3![]() ,BH=OH﹣OB=2
,BH=OH﹣OB=2![]() ,
,
又OC≤3,则tan∠OHC=![]() ≤
≤![]() ,
,
于是0<∠OHC<30°,
则h=BF=BHsin∠BHF≤BHsin30°=![]() ,
,
从而0<h≤![]() .
.
(3)当a取最大值时,a=![]() ,
,
此时h=![]() ,B(
,B(![]() ,0),C(0,﹣3),D(-
,0),C(0,﹣3),D(-![]() ,﹣4),
,﹣4),
可求BD=2![]() ,BC=2
,BC=2![]() ,
,
作直径DG,易证△DGB∽△BCF,![]() ,
,

所以![]() .
.
故DG=4![]() ,
,
即△BCD外接圆的半径为2![]() .
.

练习册系列答案
相关题目