Question

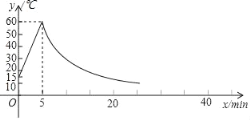
【题目】制作一种产品，需先将材料加热达到60℃后，再进行操作，设该材料温度为y（℃）从加热开始计算的时间为x（min）．据了解，当该材料加热时，温度y与时间x成一次函数关系：停止加热进行操作时，温度y与时间x成反比例关系（如图）．已知在操作加热前的温度为15℃，加热5分钟后温度达到60℃．

（1）分别求出将材料加热和停止加热进行操作时，y与x的函数关系式；

（2）根据工艺要求，当材料的温度低于15℃时，须停止操作，那么从开始加热到停止操作，共经历了多少时间？

Answer 1

【答案】（1）y＝；（2）20分钟

【解析】

1）当0≤x≤5时，设一次函数解析式为y＝kx+b，把（0，15），（5，60）代入，然后解关于k、b的方程组即可；当x＞5时，设反比例函数解析式为y＝，把（5，60）代入求出m即可得到反比例函数解析式；

（2）计算y＝15时所对应的反比例函数值即可．

（1）当0≤x≤5时，

设一次函数解析式为y＝kx+b，

把（0，15），（5，60）代入得，

，

解得，，

所以一次函数解析式为y＝9x+15；

当x＞5时，设反比例函数解析式为y＝，

把（5，60）代入得m＝5×60＝300，

所以反比例函数解析式为y＝；

（2）当y＝15时，＝15，解得x＝20，

所以从开始加热到停止操作，共经历了20分钟．