题目内容

【题目】已知A、B两地相距40千米，中午12：00时，甲从A地出发开车到B地，12：10时乙从B地出发骑自行车到A地，设甲行驶的时间为t（分），甲、乙两人离A地的距离S（千米）与时间t（分）之间的关系如图所示．由图中的信息可知，乙到达A地的时间为（ ）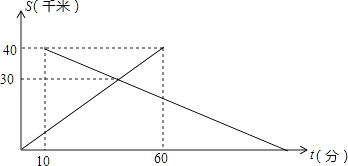

A.14：00
B.14：20
C.14：30
D.14：40

【答案】C
【解析】因为甲60分走完全程0千米，所以甲的速度是 千米/分，

由图中看出两人在走了30千米时相遇，那么甲此时用了30÷ =45分，则乙用了（45-10）=35分，

所以乙的速度为：（40-30）÷35= 千米/分，所以乙走完全程需要时间为：40÷= 140分，此时的时间应加上乙先前迟出发的10分，现在的时间为14：点30分；

故答案为：C.

根据图像得到甲60分走完全程0千米，求出甲的速度，由图中看出两人在走了30千米时相遇，求出甲此时用的时间和乙用的时间，求出乙的速度和乙走完全程需要的时间，求出乙到达A地的时间.

练习册系列答案
相关题目

【题目】为了保护环境，某公交公司决定购买A、B两种型号的全新混合动力公交车共10辆，其中A种型号每辆价格为a万元，每年节省油量为万升；B种型号每辆价格为b万元，每年节省油量为万升：经调查，购买一辆A型车比购买一辆B型车多20万元，购买2辆A型车比购买3辆B型车少60万元．

请求出a和b；

若购买这批混合动力公交车每年能节省万升汽油，求购买这批混合动力公交车需要多少万元？

【答案】（1）；（2）购买这批混合动力公交车需要1040万元．

【解析】

(1)根据“购买一台A型车比购买一台B型车多20万元，购买2台A型车比购买3台B型车少60万元.”即可列出关于a、b的二元一次方程组，解之即可得出结论；

(2)设A型车购买x台，B型车购买y台，根据总节油量=2.4×A型车购买的数量+2.2×B型车购买的数量、A型车数量+B型车数量=10得出方程组，解之求得x和y的值，再根据总费用=120×A型车购买的数量+100×B型车购买的数量即可算出购买这批混合动力公交车的总费用．

解：根据题意得：，

解得：;

设A型车购买x台，B型车购买y台，

根据题意得：，

解得：，

万元．

答：购买这批混合动力公交车需要1040万元．

【点睛】

本题考查了二元一次方程组的应用，根据题意找出等量关系列出方程组是解题的关键.

【题型】解答题
【结束】
16

【题目】在边长为1的正方形网格中

作出关于直线MN对称的；

若经过图形平移得到，当点A的坐标是时，请建立适当的直角坐标系，分别写出点，，的坐标．

【题目】某商场的一种书法笔每只售价25元,书法练习本每本售价5元。为促销,商场制定了两种优惠方案：买一支书法笔就赠送一本书法练习本;方案二：按够买金额的九折付款,我校书法社团够买10支书法笔,x(x>10)本练习本。

(1)请你写出两种优惠方案的实际付款金额y(元)与x(本)之间的关系式。

(2)当购买多少本书法练习本时，两种优惠方案的实付金额一样?

【题目】下列四个函数中，y的值随着x值的增大而减小的是（ ）
A.y=2x
B.y=x+1
C.y= （x＞0）
D.y=x2（x＞0）

【题目】如图，抛物线的顶点D的坐标为（1，﹣4），与y轴交于点C（0，﹣3），与x轴交于A、B两点．

（1）求该抛物线的函数关系式；
（2）在抛物线上存在点P（不与点D重合），使得S△PAB=S△ABD ， 请求出P点的坐标．

【题目】解下列方程．

（1）x2﹣14x=8（配方法）

（2）x2﹣7x﹣18=0（公式法）

（3）（2x+3）2=4（2x+3）（因式分解法）

（4）2（x﹣3）2=x2﹣9．

【题目】小明上午8点正从家里出发，到书店买书．右图反映了小明买书过程中（从出发到回家）离家的距离y（米）和离家的时间x（分）的关系．

（1）书店离小明家多远？
（2）若小明离开书店返回家时的平均速度比去书店时的平均速度每分钟快15米，问小明几点到家并求小明离开书店后返家过程中y与x的函数关系式．

【题目】如图，在△ABC中，AB=AC，∠A=36°，BD、CE分别是∠ABC、∠BCD的角平分线，则图中的等腰三角形有（　　）

A. 5个 B. 4个 C. 3个 D. 2个

【题目】如图，已知点B、C、D在同一条直线上，△ABC和△CDE都是等边三角形.BE交AC于F，AD交CE于H，

①求证：△BCE≌△ACD；

②求证：CF=CH；

③判断△CFH的形状并说明理由。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网