题目内容
【题目】如图.在△ABC中,E是AB的中点,D是AC上的一点,且AD:DC=2:3,BD与CE交于F,S△ABC=40,求SAEFD .
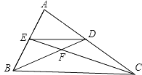
【答案】SAEFD= 11.
【解析】
四边形AEFD可分割为△AED与△DEF.从E是AB中点及D分AC为2:3的条件看,△AED的面积不难推知,关键是如何推求△DEF的面积.为此,需通过添加辅助线的办法,寻求△DEF的面积与已知面积的关系
取AD的中点G,并连接EG在△ABD中,E是AB的中点,
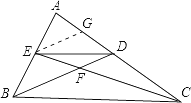
由题知EG∥BD.又CD:DG=3:1,
从而,在△CEG中,CF:FE=CD:DG=3:1,
∴S△DFC:S△DFE=3:1.
设S△DEF=x,则S△DFC=3x,S△DEC=4x.
由于AD:DC=2:3,
∴S△EAD:S△ECD=2:3,
∴S△EAD= ![]() S△DEC=
S△DEC= ![]() x,
x,
S△ACE= ![]() x+4x=
x+4x= ![]() x,
x,
又因为E是AB中点,
所以S△ACE= ![]() S△ABC=20,
S△ABC=20,
∴ ![]() x=20,
x=20,
解得x=3,即S△DEF=3,
∴S△ADE= ![]() x=8,
x=8,
∴SAEFD=S△ADE+S△DEF=8+3=11.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目