题目内容
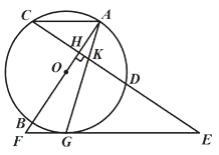
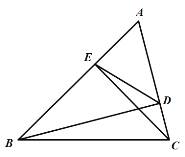
【题目】如图,BD、CE是△ABC的高.
(1)试说明B、C、D、E四点在同一个圆上;
(2)若S△ADE∶S△ABC=1∶4,BC=8,求DE的长.
【答案】(1)证明见解析;(2)DE=4 .
【解析】
(1)取BC中点O,连接OE,OD,根据四点共圆的判定证明即可;
(2)根据相似三角形的判定和性质解答即可.
(1)取BC中点O,连接OE,OD.
∵BD,CE为两边上的高,O为斜边上的中点,∴OB=OE=OD=OC,∴B、E、D、C四点共圆,即B、C、D、E四点在同一个圆上.
(2)∵B、E、D、C四点共圆,∴∠ABC+∠EDC=180°.
∵∠ADE+∠EDC=180°,∴∠ADE=∠ABC.
在△ADE与△ABC中,∵∠A=∠A,∠ABC=∠ADE,∴△ADE∽△ABC,∴![]() .
.
∵S△ADE:S△ABC=1:4,∴![]() .
.
∵BC=8,∴DE=4.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目