题目内容
【题目】如图,在平面直角坐标系中,以A(3,0)为圆心,以5为半径的圆与x轴相交于B. C,与y轴的负半轴相交于D,抛物线y=x![]() +bx+c经过B. C. D三点。
+bx+c经过B. C. D三点。
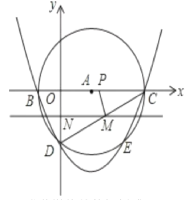
(1)求此抛物线的解析式;
(2)若动直线MN(MN∥x轴)从点D开始,以每秒1个长度单位的速度沿y轴的正方向移动,且与线段CD、y轴分别交于M、N两点,动点P同时从点C出发,在线段OC上以每秒2个长度单位的速度向原点O运动,连接PM,设运动时间为t秒,若以P、C. M为顶点的三角形与△OCD相似,求实数t的值;
②当t为何值时,![]() 的值最大,并求出最大值。
的值最大,并求出最大值。
【答案】(1)y=![]() x
x![]()
![]() x4;(2)t=2或t=
x4;(2)t=2或t=![]() ,②当t=2时取最大值2;
,②当t=2时取最大值2;
【解析】
(1)直接利用圆的性质得出B,C点坐标,进而利用交点式求出函数解析式;
(2)①直接利用若△PCM∽△OCD或△MCP∽△OCD,分别得出t的值求出答案即可;
②利用MN∥OC,则![]() ,进而求出
,进而求出![]() 关于t的关系式求出最值即可.
关于t的关系式求出最值即可.
(1)∵A(3,0)为圆心,以5为半径的圆与x轴相交于B. C,
∴B(2,0),C(8,0),
代入抛物线y=![]() (x+2)(x8),
(x+2)(x8),
得y=![]() x
x![]()
![]() x4;
x4;
(2)①由题可得N(0,t4),P(82t,0),
若△PCM∽△OCD,
则![]() ,即
,即![]() ,
,
解得t=2;
若△MCP∽△OCD,则![]() ,即
,即![]() ,
,
解得t=![]() ,
,
即当t=2或t=![]() 时,以P、C. M为顶点的三角形与△OCD相似。
时,以P、C. M为顶点的三角形与△OCD相似。
②∵MN∥OC,
![]() ,即MN=2t,
,即MN=2t,
又∵OP=82t,
∴![]() ,
,
∴当t=2时取最大值2.

练习册系列答案
相关题目