题目内容
（1）当a=5，b=2时，求下列代数式的值：
①（a+b）（a-b）； ②a2-b2；
通过以上的计算，你发现①、②两个式子的值有何关系？
（2）当a=-5，b=-2，上述结论是否仍然成立？
（3）综合（1）（2）写出①②的关系式，并利用这个关系式求1002-992+982-972+…+22-1等于多少？
解：（1）①（a+b）（a-b）=（5+2）×（5-2）=21；
②a2-b2=52-22=25-4=21；
通过以上的计算，你发现①、②两个式子的值相等；
（2）当a=-5，b=-2时，（a+b）（a-b）=（-5-2）×（-5+2）=21；a2-b2=25-4=21，
通过以上的计算，你发现①、②两个式子的值相等；
（3）根据题意得：1002-992+982-972+…+22-1=199+195+191+…+3=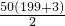
=5050．
分析：（1）将a=5，b=2代入两式计算得到结果，即可做出判断；
（2）将a=-5，b=-2代入两式计算得到结果，即可做出判断；
（3）利用前面总结的结论化简所求式子，求出之和即可．
点评：此题考查了代数式求值，得出公式a2-b2=（a+b）（a-b）是解本题的关键．
②a2-b2=52-22=25-4=21；
通过以上的计算，你发现①、②两个式子的值相等；
（2）当a=-5，b=-2时，（a+b）（a-b）=（-5-2）×（-5+2）=21；a2-b2=25-4=21，
通过以上的计算，你发现①、②两个式子的值相等；
（3）根据题意得：1002-992+982-972+…+22-1=199+195+191+…+3=
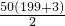=5050．分析：（1）将a=5，b=2代入两式计算得到结果，即可做出判断；
（2）将a=-5，b=-2代入两式计算得到结果，即可做出判断；
（3）利用前面总结的结论化简所求式子，求出之和即可．
点评：此题考查了代数式求值，得出公式a2-b2=（a+b）（a-b）是解本题的关键．
练习册系列答案
相关题目
如图，在△ABC中，已知AB=BC=CA=4cm，AD⊥BC于D．点P、Q分别从B、C两点同时出发，其中点P沿BC向终点C运动，速度为1cm/s；点Q沿CA、AB向终点B运动，速度为2cm/s，设它们运动的时间为x（s）．
水管．如图表示水塔中的储水量Q（米3）与时间t（小时）之间的函数图象．
？试写出你的猜想，并说明理由．
