题目内容
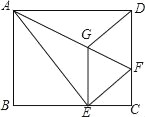
【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2)试证明EG2=![]() GFAF.
GFAF.
【答案】(1)见解析;(2)见解析.
【解析】
(1)先依据翻折的性质和平行线的性质证明∠DGF=∠DFG,从而得到GD=DF,接下来依据翻折的性质可证明DG=GE=DF=EF;
(2)连接DE,交AF于点O.由菱形的性质可知GF⊥DE,OG=OF=![]() GF,接下来,证明△DOF∽△ADF,由相似三角形的性质可证明DF2=FOAF,于是可得到GE、AF、FG的数量关系.
GF,接下来,证明△DOF∽△ADF,由相似三角形的性质可证明DF2=FOAF,于是可得到GE、AF、FG的数量关系.
(1)证明:∵GE∥DF,
∴∠EGF=∠DFG.
∵由翻折的性质可知:GD=GE,DF=EF,∠DGF=∠EGF,
∴∠DGF=∠DFG.
∴GD=DF.
∴DG=GE=DF=EF.
∴四边形EFDG为菱形.
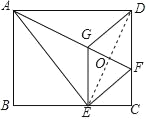
(2)解:如图所示:连接DE,交AF于点O.
∵四边形EFDG为菱形,
∴GF⊥DE,OG=OF=![]() GF.
GF.
∵∠DOF=∠ADF=90°,∠OFD=∠DFA,
∴△DOF∽△ADF.
∴![]() ,即DF2=FOAF.
,即DF2=FOAF.
∵FO=![]() GF,DF=EG,
GF,DF=EG,
∴EG2=![]() GFAF.
GFAF.

 阅读快车系列答案
阅读快车系列答案【题目】(9分)某市球类运动协会为了筹备一次大型体育活动,购进了一定数量的体育器材,器材管理员对购买的部分器材进行了统计,表1和图2是器材管理员通过采集数据后,绘制的两幅不完整的频率分布表与频数分布直方图.请你根据图表中提供的信息,解答以下问题:
频率分布表
器材种类 | 频数 | 频率 |
排 球 | 20 | |
乒乓球拍 | 50 | 0.50 |
篮 球 | 25 | 0.25 |
足 球 | ||
合 计 | 1 |
![]()
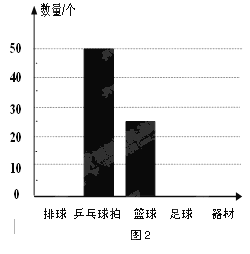
(1)填充图1频率分布表中的空格.
(2)在图2中,将表示“排球”和“足球”的部分补充完整.
(3)已知该协会购买这批体育器材时,篮球和足球一共花去950元,且足球每个的价格比篮球多10元.现准备再采购篮球和足球这两种球共10个(两种球的个数都不能为0),计划资金不超过320元,试问该协会有哪几种购买方案?