题目内容
【题目】如图,甲、乙两人同时沿着边长为100m的正方形广场ABCD , 按A→B→C→D→A…的顺序跑,甲从A出发,速度为82m/min,乙从B出发,速度为90m/min,则当乙第一次追到甲时,他在正方形广场( ) 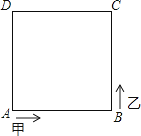
A.AB边
B.BC边
C.CD边
D.AD边
【答案】C
【解析】解答:设当乙第一次追到甲时乙用了x分钟,由题意,得 90x=82x+300,
解得: ![]() .
.
∴乙行驶的路程为:90× ![]() =3375米.
=3375米.
∴乙行驶的边数为:3375÷100=33.75≈34边.
∵34÷4=8余2.
∴乙走了8圈多两边追到甲,
∴乙第一次追到甲时,他在正方形广场的CD边上.
故选:C.
分析:设当乙第一次追到甲时乙用了x分钟,由甲走的路程+300=乙走的路程建立方程求出其解即可.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目