Question

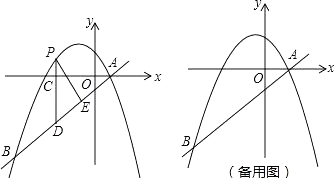
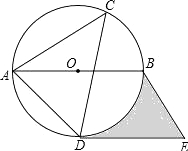
【题目】如图，⊙O是△ACD的外接圆，AB是直径，过点D作直线DE∥AB，过点B作直线BE∥AD，两直线交于点E，如果∠ACD=45°，⊙O的半径是4cm，

（1）请判断DE与⊙O的位置关系，并说明理由；

（2）求图中阴影部分的面积（结果用π表示）．

Answer 1

【答案】（1）DE与⊙O相切．理由详见解析；(2)（24﹣4π）．

【解析】

试题分析：（1）连结OD，根据圆周角定理得∠ABD=∠ACD=45°，∠ADB=90°，可判断△ADB为等腰直角三角形，所以OD⊥AB，而DE∥AB，则有OD⊥DE，然后根据切线的判定定理得到DE为⊙O的切线；

（2）先由BE∥AD，DE∥AB得到四边形ABED为平行四边形，则DE=AB=8cm，然后根据梯形的面积公式和扇形的面积公式利用进行计算即可．

试题解析：（1）DE与⊙O相切．理由如下：

连结OD，BD，则∠ABD=∠ACD=45°，

∵AB是直径，

∴∠ADB=90°，

∴△ADB为等腰直角三角形，

∵点O为AB的中点，

∴OD⊥AB，

∵DE∥AB，

∴OD⊥DE，

∵OD是半径，

∴DE为⊙O的切线；

（2）∵BE∥AD，DE∥AB，

∴四边形ABED为平行四边形，

∴DE=AB=8cm，

∴=×（4+8）×4﹣=（24﹣4π）．