题目内容
【题目】如图,在Rt△ABC中,∠C=90°,∠A=60°,AB=12cm,若点P从点B出发以2cm/s的速度向点A运动,点Q从点A出发以1cm/s的速度向点C运动,设P、Q分别从点B、A同时出发,运动的时间为ts. 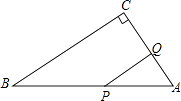
(1)用含t的式子表示线段AP、AQ的长;
(2)当t为何值时,△APQ是以PQ为底边的等腰三角形?
(3)当t为何值时,PQ∥BC?
【答案】
(1)解:∵Rt△ABC中,∠C=90°,∠A=60°,
∴∠B=30°.
又∵AB=12cm,
∴AC=6cm,BP=2t,AP=AB﹣BP=12﹣2t,AQ=t
(2)解:∵△APQ是以PQ为底的等腰三角形,
∴AP=AQ,即12﹣2t=t,
∴当t=4时,△APQ是以PQ为底边的等腰三角形
(3)解:当PQ⊥AC时,PQ∥BC.
∵∠C=90°,∠A=60°,
∴∠B=30°
∵PQ∥BC,
∴∠QPA=30°
∴AQ= ![]() AP,
AP,
∴t= ![]() (12﹣2t),解得t=3,
(12﹣2t),解得t=3,
∴当t=3时,PQ∥BC
【解析】(1)由题意,可知∠B=30°,AC=6cm.BP=2t,AP=AB﹣BP,AQ=t.(2)若△APQ是以PQ为底的等腰三角形,则有AP=AQ,即12﹣2t=t,求出t即可.(3)先根据直角三角形的性质求出∠B的度数,再由平行线的性质得出∠QPA的度数,根据直角三角形的性质即可得出结论.
【考点精析】认真审题,首先需要了解平行线的判定(同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行),还要掌握等腰三角形的判定(如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等)的相关知识才是答题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目