题目内容
【题目】如图, ![]() 是⊙
是⊙ ![]() 的直径,
的直径, ![]() 是⊙
是⊙ ![]() 的弦,过点
的弦,过点 ![]() 的切线交
的切线交 ![]() 的延长线于点
的延长线于点 ![]() ,且
,且 ![]() .
.
(1)求 ![]() 的度数;
的度数;
(2)若 ![]() =3,求图中阴影部分的面积.
=3,求图中阴影部分的面积.
【答案】
(1)解:连接OC,
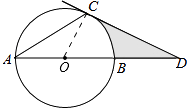
∵过点C的切线交AB的延长线于点D,
∴OC⊥CD,
∴∠OCD=90°,即∠D+∠COD=90°,
∵AO=CO,
∴∠A=∠ACO,
∴∠COD=2∠A,
∵∠A=∠D,
∴∠COD=2∠D,
∴3∠D=90°,
∴∠D=30°,
∴∠ACD=180°-∠A-∠D=180°-30°-30°=120°
(2)解:由(1)可知∠COD=60°在Rt△COD中,∵CD=3,∴OC=3× ![]() ,∴阴影部分的面积=
,∴阴影部分的面积= ![]()
【解析】(1)根据切线的性质和已知∠A=∠D,得到∠COD=2∠D,根据三角形内角和定理,求出∠ACD的度数;(2)由(1)可知∠COD=60°,求出阴影部分的面积等于三角形COD的面积-扇形COB的面积.
【考点精析】利用切线的性质定理对题目进行判断即可得到答案,需要熟知切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目





