Question

【题目】如图，已知正方形OABC的边长为2，顶点A，C分别在x轴，y轴的正半轴上，E点是BC的中点，F是AB延长线上一点且FB=1．

（1）求经过点O，A，E三点的抛物线解析式；
（2）点P在抛物线上运动，当点P运动到什么位置时△OAP的面积为2，请求出点P的坐标；
（3）在抛物线上是否存在一点Q，使△AFQ是等腰直角三角形？若存在直接写出点Q的坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）解：A的坐标是（2，0），E的坐标是（1，2）．

设抛物线的解析式是y=ax2+bx+c，

根据题意得： ，

解得： ．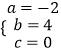

则抛物线的解析式是y=﹣2x2+4x

（2）解：当△OAP的面积是2时，P的纵坐标是2或﹣2．

当﹣2x2+4x=2时，解得：x=1，则P的坐标是（1，2）；

当﹣2x2+4x=﹣2时，解得：x=1± ，

此时P的坐标是（1+ ，﹣2）或（1﹣ ，﹣2）

（3）解：AF=AB+BF=2+1=3．

OA=2，则A是直角顶点时，Q不可能在抛物线上；

当F是直角顶点时，Q不可能在抛物线上；

当Q是直角顶点时，Q到AF的距离是 AF= ，若Q存在，则Q的坐标是（2﹣ ， ），即（ ， ），在抛物线上；

综上，抛物线上存在Q点满足题目要求

【解析】（1）先求出A、O、E三点的坐标，利用待定系数法代入解析式即可；（2）因为OA=2，所以当△OAP的面积是2时，就是P到x轴的距离是2，即P的纵坐标是2或﹣2，即﹣2x2+4x=2或2x2+4x=﹣2解方程；（3）△AFQ是等腰直角三角形可分类讨论：A是直角顶点；F是直角顶点；Q是直角顶点；