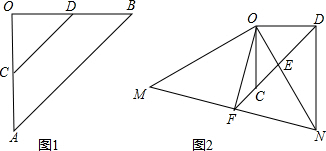
��Ŀ����
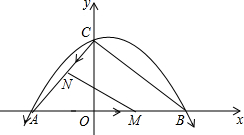 ��2013•��ƽ��ģ�⣩��ͼ��������y=ax2+
��2013•��ƽ��ģ�⣩��ͼ��������y=ax2+| 1 | 3 |
��1����������ߵĽ���ʽ��
��2����M���߶�AB����ÿ��2����λ���ȵ��ٶȴӵ�A���B�˶���ͬʱ����N���߶�AC����ÿ��1����λ���ȵ��ٶȴӵ�C���A�˶������˶�ʱ��Ϊt��0��t��3.5����������ı���BCNM�����S��t�ĺ�����ϵʽ����tΪ��ֵʱ��S��ֵ��С����Сֵ�Ƕ��٣�
��3����P�������߶Գ����ϣ���Q���������ϣ��ڣ�2���������£����ı���BCNM�����S��Сʱ���Ƿ���������ĵ�P���Q��ʹ��P��Q��B��NΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д����P�����꣨��д�����̣����������ڣ���˵�����ɣ�
��������1����A��-3��0����B��4��0���������������y=ax2+
x+c��a��0��������������ʽ���a��c��ֵ���Ӷ�����������ߵĽ���ʽ��
��2�������⣬��AM=2t��CN=t�����ݹ��ɶ�������AC����ʾ��AN����ND��OA�ڵ�D���������������ε����ʿɱ�ʾ��DN�����������ε�������ɵõ��ı���BCNM�����S��t�ĺ�����ϵʽ���䷽�����S����Сֵ��
��3������ƽ���ı��ε����ʽ��ͼ�εó�����BNΪ�Խ����Լ���BNΪһ��ʱ���ֱ�ó�P�����꼴�ɣ�
| 1 |
| 3 |
��2�������⣬��AM=2t��CN=t�����ݹ��ɶ�������AC����ʾ��AN����ND��OA�ڵ�D���������������ε����ʿɱ�ʾ��DN�����������ε�������ɵõ��ı���BCNM�����S��t�ĺ�����ϵʽ���䷽�����S����Сֵ��
��3������ƽ���ı��ε����ʽ��ͼ�εó�����BNΪ�Խ����Լ���BNΪһ��ʱ���ֱ�ó�P�����꼴�ɣ�
����⣺��1��������y=ax2+
x+c����A��-3��0����B��4��0�����㣬��
��
���
��
�������ߵĽ���ʽΪy=-
x2+
x+4��
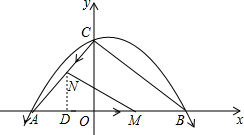
��2�������⣬��AM=2t��CN=t��
��OC=4��OA=3����AOC=90�㣬
��AC=
=
=5��
��AN=AC-CN=5-t��
��ND��OA�ڵ�D��
��OC��OA��
��ND��OC��
��
=
��
 ��DN=
��DN=
=
(5-t)��
��S=S��ABC-S��AMN
=
AB•OC-
AM•DN
=
��7��4-
��2t��
(5-t)
=
t2-4t+14��
��S=
(t-
)2+9��
�൱t=
ʱ��S����Сֵ��9��
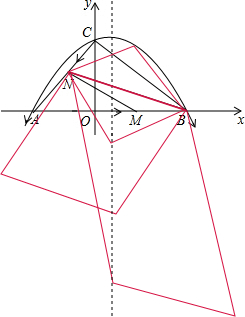
��3����ͼ�����ڣ�
����BNΪ�Խ��ߣ�N������Ϊ��-
��2������Q��ĺ�����Ϊ4-��
+
��=2����x=2ʱ��y=-
��22+
��2+4=3
�����P��������Ϊ2-3
=-
���ʵ�P������Ϊ��
��-
����
����BNΪһ�ߣ���Q��ĺ�����Ϊ
-��4+
��=-5����x=-5ʱ��y=-
����-5��2+
����-5��+4=-6�����P��������Ϊ-6+2=-4���ʵ�P������Ϊ��
��-4����
����BNΪһ�ߣ���Q��ĺ�����Ϊ
+��4+
��=6����x=6ʱ��y=-
��62+
��6+4=-6�����P��������Ϊ-6-2=-8���ʵ�P������Ϊ��
��-8����
�ʵ�P������Ϊ��
��-
������
��-4������
��-8����
| 1 |
| 3 |
|
���
|
�������ߵĽ���ʽΪy=-
| 1 |
| 3 |
| 1 |
| 3 |

��2�������⣬��AM=2t��CN=t��
��OC=4��OA=3����AOC=90�㣬
��AC=
| OC2+OA2 |
| 42+32 |
��AN=AC-CN=5-t��
��ND��OA�ڵ�D��
��OC��OA��
��ND��OC��
��
| DN |
| OC |
| AN |
| AC |
 ��DN=
��DN=| AN•OC |
| AC |
| 4 |
| 5 |
��S=S��ABC-S��AMN
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 5 |
=
| 4 |
| 5 |
��S=
| 4 |
| 5 |
| 5 |
| 2 |
�൱t=
| 5 |
| 2 |
��3����ͼ�����ڣ�
����BNΪ�Խ��ߣ�N������Ϊ��-
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
����BNΪһ�ߣ���Q��ĺ�����Ϊ
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
����BNΪһ�ߣ���Q��ĺ�����Ϊ
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
�ʵ�P������Ϊ��
| 1 |
| 2 |
| 4 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
������������Ҫ�����˶��κ������ۺ�Ӧ���Լ�ƽ���ı��ε��������ж��������������֪ʶ��������֪���ͼ���Լ����÷�������˼��ó��ǽ���ؼ���

��ϰ��ϵ�д�
 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
�����Ŀ
 ��2013•��ƽ��ģ�⣩ľ��ʦ���������ſ��Ϊ��ֹ���γ�����ͼ����ʾ������������б����ľ��������ͼ�е�AB��CD�����������ĸ����ǣ�������
��2013•��ƽ��ģ�⣩ľ��ʦ���������ſ��Ϊ��ֹ���γ�����ͼ����ʾ������������б����ľ��������ͼ�е�AB��CD�����������ĸ����ǣ������� ��2013•��ƽ��ģ�⣩һ����Ȼ�������������Է��ѳ����ɸ����������ĺͣ����磺23��33��43�ֱ������ͼ��ʾ�ķ�ʽ�����ѡ���2����3����4�����������ĺͣ���23=3+5��33=7+9+11��43=13+15+17+19��������73Ҳ���մ˹��������С����ѡ�����73�����ѡ����������У�����������
��2013•��ƽ��ģ�⣩һ����Ȼ�������������Է��ѳ����ɸ����������ĺͣ����磺23��33��43�ֱ������ͼ��ʾ�ķ�ʽ�����ѡ���2����3����4�����������ĺͣ���23=3+5��33=7+9+11��43=13+15+17+19��������73Ҳ���մ˹��������С����ѡ�����73�����ѡ����������У�����������