题目内容
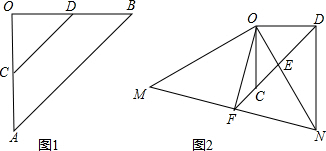
（2013•金平区模拟）如图1，在Rt△OAB中，∠AOB=90°，OA=OB=2
，点C、点D分别在OA、OB上，OC=OD=2．如图2，Rt△OAB绕点O顺时针旋转角θ（0°＜θ＜90°），得到△OMN．连接DN，若ND⊥OD，ON与CD交于点E．
（1）求tanθ的值；
（2）求DE的长；
（3）延长DC交MN于点F，连接OF，请你确定线段OF与线段MN的关系，并说明理由．
| 5 |
（1）求tanθ的值；
（2）求DE的长；
（3）延长DC交MN于点F，连接OF，请你确定线段OF与线段MN的关系，并说明理由．
分析：（1）根据勾股定理求出DN的值，根据tanθ=tan∠DON=
代入求出即可；
（2）证△OCE∽△NDE，得出
=
，求出CE=
DE，在Rt△ODC中，由勾股定理求出DC，即可得出答案；
（3）OF=
MN，OF⊥MN．理由是：证△NFE∽△ODE，得出
=
，证△OCE∽△NDE，得出
=
=
，求出FN，根据勾股定理求出MN，即可得出F为等腰直角三角形OMN斜边MN的中点，即可得出答案．
| DN |
| OD |
（2）证△OCE∽△NDE，得出
| CE |
| DE |
| OC |
| DN |
| 1 |
| 2 |
（3）OF=
| 1 |
| 2 |
| FN |
| OD |
| EN |
| ED |
| OE |
| NE |
| OC |
| DN |
| 2 |
| 4 |
解答：解：（1）在Rt△ODN中，OD=2，ON=OB=2
，
∴DN=
=
=4，
∴tanθ=tan∠DON=
=
=2；
（2）∵∠AOD=90°，
∴OC⊥OD，
∵ND⊥OD，
∴OC∥DN，
∴△OCE∽△NDE，
∴
=
，
∵OC=2，DN=4，
∴CE=
DE，
在Rt△ODC中，DC=
=
=2
，
∴DE=
DC=
；
（3）OF=
MN，OF⊥MN．理由是：
∵∠FNE=∠ODE=45°，∠FEN=∠OED，
∴△NFE∽△ODE，
∴
=
，
由（2）得△OCE∽△NDE，
∴
=
=
，
∴OE=
NE，
∴NE=
ON=
，
∴FN=
×OD=
×2=
，
∵在Rt△OMN中，MN=
=
=2
，
∴FN=
MN，
∴F为等腰直角三角形OMN斜边MN的中点，
∴OF=
MN，OF⊥MN．
| 5 |
∴DN=
| ON2-OD2 |
| 20-4 |
∴tanθ=tan∠DON=
| DN |
| OD |
| 4 |
| 2 |
（2）∵∠AOD=90°，∴OC⊥OD，
∵ND⊥OD，
∴OC∥DN，
∴△OCE∽△NDE，
∴
| CE |
| DE |
| OC |
| DN |
∵OC=2，DN=4，
∴CE=
| 1 |
| 2 |
在Rt△ODC中，DC=
| OC2+OD2 |
| 22+22 |
| 2 |
∴DE=
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
（3）OF=
| 1 |
| 2 |
∵∠FNE=∠ODE=45°，∠FEN=∠OED，
∴△NFE∽△ODE，
∴
| FN |
| OD |
| EN |
| ED |
由（2）得△OCE∽△NDE，
∴
| OE |
| NE |
| OC |
| DN |
| 2 |
| 4 |
∴OE=
| 1 |
| 2 |
∴NE=
| 2 |
| 3 |
| 4 |
| 3 |
| 5 |
∴FN=
| EN |
| ED |
| ||||
|
| 10 |
∵在Rt△OMN中，MN=
| OM2+ON2 |
(2
|
| 10 |
∴FN=
| 1 |
| 2 |
∴F为等腰直角三角形OMN斜边MN的中点，
∴OF=
| 1 |
| 2 |
点评：本题考查了等腰直角三角形性质，勾股定理，相似三角形的性质和判定的应用，主要考查学生运用性质进行推理和计算的能力．
练习册系列答案
天天向上口算本系列答案
相关题目
（2013•金平区模拟）木工师傅在做完门框后，为防止变形常常像图中所示那样钉上两条斜拉的木板条（即图中的AB和CD），这样做的根据是（ ）
（2013•金平区模拟）一个自然数的立方，可以分裂成若干个连续奇数的和．例如：23，33和43分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和，即23=3+5；33=7+9+11；43=13+15+17+19；…；若73也按照此规律来进行“分裂”，则73“分裂”出的奇数中，最大的奇数是