题目内容
【题目】已知:A、O、B三点在同一条直线上,过O点作射线OC,使∠AOC:∠BOC=1:2,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
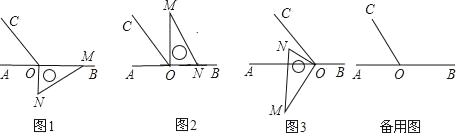
(1)将图1中的三角板绕点O按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为 度;
(2)继续将图2中的三角板绕点O按逆时针方向旋转至图3的位置,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)将图1中的三角板绕点O按5°每秒的速度沿逆时针方向旋转一周的过程中,当直角三角板的直角边OM所在直线恰好平分∠BOC时,时间t的值为 (直接写结果).
【答案】(1)90°;(2)30°;(3)12秒或48秒.
【解析】
(1)依据图形可知旋转角=∠NOB,从而可得到问题的答案;
(2)先求得∠AOC的度数,然后依据角的和差关系可得到∠NOC=60°-∠AON,∠AOM=90°-∠AON,然后求得∠AOM与∠NOC的差即可;
(3)可分为当OM为∠BOC的平分线和当OM的反向延长为∠BOC的平分线两种情况,然后再求得旋转的角度,最后,依据旋转的时间=旋转的角度÷旋转的速度求解即可.
(1)由旋转的定义可知:旋转角=∠NOB=90°.
故答案为:90°
(2)∠AOM﹣∠NOC=30°.
理由:∵∠AOC:∠BOC=1:2,∠AOC+∠BOC=180°,
∴∠AOC=60°.
∴∠NOC=60°﹣∠AON.
∵∠NOM=90°,
∴∠AOM=90°﹣∠AON,
∴∠AOM﹣∠NOC=(90°﹣∠AON)﹣(60°﹣∠AON)=30°.
(3)如图1所示:当OM为∠BOC的平分线时,
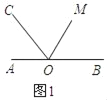
∵OM为∠BOC的平分线,
∴∠BOM=![]() ∠BOC=60°,
∠BOC=60°,
∴t=60°÷5°=12秒.
如图2所示:当OM的反向延长为∠BOC的平分线时,

∵ON为为∠BOC的平分线,
∴∠BON=60°.
∴旋转的角度=60°+180°=240°.
∴t=240°÷5°=48秒.
故答案为:12秒或48秒.

 名校课堂系列答案
名校课堂系列答案【题目】为了打造区域中心城市,实现攀枝花跨越式发展,我市花城新区建设正按投资计划有序推进.花城新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3 , 现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如下表所示:
租金(单位:元/台时) | 挖掘土石方量(单位:m3/台时) | |
甲型挖掘机 | 100 | 60 |
乙型挖掘机 | 120 | 80 |
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有哪几种不同的租用方案?