题目内容
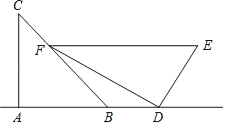
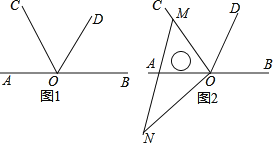
【题目】如图1,点O为直线AB上一点,过点O作射线OC,OD,使射线OC平分∠AOD.
(1)当∠BOD=50°时,∠COD= °;
(2)将一直角三角板的直角顶点放在点O处,当三角板MON的一边OM与射线OC重合时,如图2.
①在(1)的条件下,∠AON= °;
②若∠BOD=70°,求∠AON的度数;
③若∠BOD=α,请直接写出∠AON的度数(用含α的式子表示).
【答案】(1)65°;(2)①25°;②35°;③![]()
【解析】
(1)由题意可得![]() COD=
COD=![]() ,
,![]() AOD=
AOD=![]() AOB-
AOB-![]() BOD.
BOD.
(2)①由(1)可得∠AOC=∠COD=65°,∠AON=90°﹣∠AOC=25°
②同①可得,∠AOC=∠COD=55°,∠AON=90°﹣∠AOC=35°
③根据(2)可直接得出结论.
解:(1)∠AOD=180°﹣∠BOD=130°,
∵OC平分∠AOD,
∴∠COD=![]() =65°.
=65°.
故答案为:65°;
(2)①由(1)可得∠AOC=∠COD=65°,
∴∠AON=90°﹣∠AOC=25°,
故答案为:25°;
②∵∠BOD=70°,
∴∠AOD=180°﹣∠BOD=110°,
∵OC平分∠AOD,
∴∠AOC=![]() ,
,
∵∠MON=90°,
∴∠AON=90°﹣∠AOC=35°;
③ ![]() .
.

练习册系列答案
相关题目