题目内容
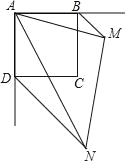
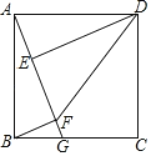
【题目】如图,在正方形ABCD中,点G在边BC上(不与点B,C重合),连接AG,作DE⊥AG于点E,BF⊥AG于点F,设![]() =k.
=k.
(1)求证:AE=BF;
(2)求证:![]() =k;
=k;
(3)连接DF,当∠EDF=30°时,求k的值.
【答案】(1)见解析;(2)见解析;(3)k=![]() .
.
【解析】
(1)根据题意可证明△ABF≌△DAE,从而证明AE=BF;
(2)根据题意可证明△ABG∽△DEA,从而可得![]() ,再由(1)的结论可得
,再由(1)的结论可得![]() =k;
=k;
(3)由(1)和(2)的结论可设DE=a,可得到EF=a﹣ka,在Rt△DEF中,根据特殊角的三角函数值求k即可.
(1)证明:∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,
∴∠BAF+∠DAE=90°,
∵DE⊥AG,
∴∠ADE+∠DAE=90°,
∴∠BAF=∠ADE,
在△ABF和△DAE中,
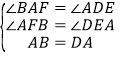 ,
,
∴△ABF≌△DAE(AAS)
∴AE=BF;
(2)证明:∵∠BAF=∠ADE,∠ABG=∠DEA,
∴△ABG∽△DEA,
∴![]() ,又AE=BF,
,又AE=BF,
∴![]() =k;
=k;
(3)解:设DE=a,
则AF=a,BF=AE=ka,
∴EF=a﹣ka,
在Rt△DEF中,tan∠EDF=![]() ,即
,即![]() ,
,
解得,k=![]() .
.

练习册系列答案
相关题目