题目内容
在数学学习过程中,通常是利用已有的知识与经验,通过对研究对象进行观察、实验、推理、抽象概括,发现数学规律,揭示研究对象的本质特征.
比如“同底数幂的乘法法则”的学习过程是利用有理数的乘方概念和乘法结合律,由“特殊”到“一般”进行抽象概括的:22×23=25,23×24=27,22×26=28,…?2m×2n=2m+n,…?am×an=am+n(m、n都是正整数).
探索问题:
(1)比较下列各组数据的大小:
①
,②
,③
,④
,….
(2)请你根据上面的材料归纳出a、b、c(a>b>0,c>0)之间的一个数学关系式;并用已学的数学知识说明你发现结论的正确性.
(3)试用(2)中你归纳的数学关系式,解释下面生活中的一个现象:“若m克糖水里含有n克糖,再加入k克糖(仍不饱和),则糖水更甜了”.
比如“同底数幂的乘法法则”的学习过程是利用有理数的乘方概念和乘法结合律,由“特殊”到“一般”进行抽象概括的:22×23=25,23×24=27,22×26=28,…?2m×2n=2m+n,…?am×an=am+n(m、n都是正整数).
探索问题:
(1)比较下列各组数据的大小:
①
| 2 |
| 3 |
<
<
| 2+1 |
| 3+1 |
| 2 |
| 3 |
<
<
| 2+2 |
| 3+2 |
| 2 |
| 3 |
<
<
| 2+3 |
| 3+3 |
| 2 |
| 3 |
<
<
| 2+4 |
| 3+4 |
(2)请你根据上面的材料归纳出a、b、c(a>b>0,c>0)之间的一个数学关系式;并用已学的数学知识说明你发现结论的正确性.
(3)试用(2)中你归纳的数学关系式,解释下面生活中的一个现象:“若m克糖水里含有n克糖,再加入k克糖(仍不饱和),则糖水更甜了”.
分析:(1)分别进行计算即可判断出大小;
(2)根据分式的定义以及(1)的计算规律写出即可;
(3)根据糖水的浓度列出分式,然后再进行计算作出判断.
(2)根据分式的定义以及(1)的计算规律写出即可;
(3)根据糖水的浓度列出分式,然后再进行计算作出判断.
解答:解:(1)比较下列各组数据的大小:
∵
=
,
=
,
=
,
=
,
∴①
<
,②
<
,③
<
,④
<
;
(2)你根据上面的材料可得:
<
.
说明:∵
-
=
-
=
=
=
,
又∵a>b>0,c>0,
∴a+c>0,b-a<0,
∴
<0,
∴
-
<0,
即:
<
成立;
(3)∵原来糖水中糖的质量分数=
,
加入k克糖后糖水中糖的质量分数+
,
由(2)
<
可得
<
,
所以糖水更甜了.
∵
| 2+1 |
| 3+1 |
| 3 |
| 4 |
| 2+2 |
| 3+2 |
| 4 |
| 5 |
| 2+3 |
| 3+3 |
| 5 |
| 6 |
| 2+4 |
| 3+4 |
| 6 |
| 7 |
∴①
| 2 |
| 3 |
| 2+1 |
| 3+1 |
| 2 |
| 3 |
| 2+2 |
| 3+2 |
| 2 |
| 3 |
| 2+3 |
| 3+3 |
| 2 |
| 3 |
| 2+4 |
| 3+4 |
(2)你根据上面的材料可得:
| b |
| a |
| b+c |
| a+c |
说明:∵
| b |
| a |
| b+c |
| a+c |
| b(a+c) |
| a(a+c) |
| a(b+c) |
| a(a+c) |
| ab+bc-ab-ac |
| a(a+c) |
| bc-ac |
| a(a+c) |
| c(b-a) |
| a(a+c) |
又∵a>b>0,c>0,
∴a+c>0,b-a<0,
∴
| c(b-a) |
| a(a+c) |
∴
| b |
| a |
| b+c |
| a+c |
即:
| b |
| a |
| b+c |
| a+c |
(3)∵原来糖水中糖的质量分数=
| n |
| m |
加入k克糖后糖水中糖的质量分数+
| n+k |
| m+k |
由(2)
| b |
| a |
| b+c |
| a+c |
| n |
| m |
| n+k |
| m+k |
所以糖水更甜了.
点评:本题考查了分式的混合运算,读懂题目信息,熟练掌握并灵活运用整式的加减混合运算进行计算是解题的关键,也是本题的难点.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 同的关系式并给予证明.
同的关系式并给予证明.

 , ②
, ② , ③
, ③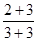 , ④
, ④ ,…。
,…。