题目内容
已知一次函数 的图象分别与坐标轴相交于A、B两点(如图所示),与反比例函数
的图象分别与坐标轴相交于A、B两点(如图所示),与反比例函数 的图象相交于C点.
的图象相交于C点.

(1)写出A、B两点的坐标;
(2)作CD⊥x轴,垂足为D,如果OB是△ACD的中位线,求反比例函数 的关系式.
的关系式.
 的图象分别与坐标轴相交于A、B两点(如图所示),与反比例函数
的图象分别与坐标轴相交于A、B两点(如图所示),与反比例函数 的图象相交于C点.
的图象相交于C点.
(1)写出A、B两点的坐标;
(2)作CD⊥x轴,垂足为D,如果OB是△ACD的中位线,求反比例函数
 的关系式.
的关系式.(1)A(﹣3,0),B(0,2);(2)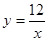
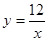
试题分析:(1)根据坐标轴上的点的坐标的特征即可求得结果;
(2)先根据OB是△ACD的中位线可得OA=OD=3,即可求得C点的坐标,从而求得结果.
(1)在
 中,当x=0时,y=2,当y=0时,x=﹣3。
中,当x=0时,y=2,当y=0时,x=﹣3。∴A的坐标是(﹣3,0),B的坐标是(0,2);
(2)∵A(﹣3,0)
∴OA=3
∵OB是△ACD的中位线
∴OA=OD=3
∴D点、C点的横坐标都是3
把x=3代入
 得:y=2+2=4,
得:y=2+2=4,∴C点的坐标是(3,4)
把C点的坐标代入
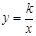 得:k=3×4=12
得:k=3×4=12∴反比例函数的关系式是
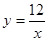 .
.点评:解答本题的关键是熟练掌握x轴上的点的纵坐标为0,y轴上的点的横坐标为0.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 x+m(m≠0)交x轴负半轴于点A、交y轴正半轴于点B且AB=5,过点A作直线AC⊥AB交y轴于点C.点E从坐标原点O出发,以0.8个单位/秒的速度沿y轴向上运动;与此同时直线l从与直线AC重合的位置出发,以1个单位/秒的速度沿射线AB方向平行移动.直线l在平移过程中交射线AB于点F、交y轴于点G.设点E离开坐标原点O的时间为t(t≥0)s.
x+m(m≠0)交x轴负半轴于点A、交y轴正半轴于点B且AB=5,过点A作直线AC⊥AB交y轴于点C.点E从坐标原点O出发,以0.8个单位/秒的速度沿y轴向上运动;与此同时直线l从与直线AC重合的位置出发,以1个单位/秒的速度沿射线AB方向平行移动.直线l在平移过程中交射线AB于点F、交y轴于点G.设点E离开坐标原点O的时间为t(t≥0)s.
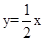 的图像相交于点(2,m).
的图像相交于点(2,m). 图像上的点,则( )
图像上的点,则( )



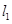 的解析式为
的解析式为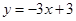 ,且
,且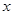 轴交于点
轴交于点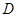 ,直线
,直线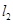 经过点
经过点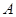 、
、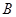 ,直线
,直线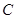 .
.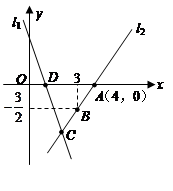
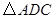 的面积;
的面积;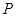 ,使得
,使得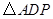 与
与 的图象向上平移,则平移后所得图象对应的函数解析式可以是 (写出一个即可).
的图象向上平移,则平移后所得图象对应的函数解析式可以是 (写出一个即可). 和
和 的图象交点为
的图象交点为 ,则不等式
,则不等式 的解集为 。
的解集为 。
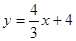 分别交x轴,y轴于A,B两点,在x轴上取一点,使△ABC为等腰三角形,则这样的点C最多有_____个。
分别交x轴,y轴于A,B两点,在x轴上取一点,使△ABC为等腰三角形,则这样的点C最多有_____个。