��Ŀ����
����Ŀ����ͼ![]() ���߳���Ϊ
���߳���Ϊ![]() ����
����![]() ����
����![]() ԭ����ȫ�غϣ���ͼ
ԭ����ȫ�غϣ���ͼ![]() ���ֱ�����
���ֱ�����![]() ������ʹ��
������ʹ��![]() �������������εĹ������ĵ�
�������������εĹ������ĵ�![]() ��˳ʱ�뷽����ת������ת�Ƕ�Ϊ
��˳ʱ�뷽����ת������ת�Ƕ�Ϊ![]() ����ע������
����ע������![]() ���еĵڢ��ʣ��������ֻҪֱ�Ӹ���������ɣ�
���еĵڢ��ʣ��������ֻҪֱ�Ӹ���������ɣ�
![]() ��
��![]() ����ʱ����
����ʱ����![]() ����
����![]() ������ת�����еĵ�һ����ȫ�غϣ�
������ת�����еĵ�һ����ȫ�غϣ�
![]() ��
��![]() ʱ��Ҫʹ��
ʱ��Ҫʹ��![]() ����
����![]() �ص����������С��
�ص����������С��![]() ����ȡ��Щ�Ƕȣ�
����ȡ��Щ�Ƕȣ�
![]() ��תʱ����ͼ
��תʱ����ͼ![]() ����
����![]() ����
����![]() ʼ�վ��й��������Բ
ʼ�վ��й��������Բ![]() ����
����![]() ʱ������
ʱ������![]() ����
����![]() �ص�����Ϊ������
�ص�����Ϊ������![]() ����
����![]() �������Χ�ڱ仯ʱ��
�������Χ�ڱ仯ʱ��
����![]() ���
���![]() ��Ӧ�ı仯��Χ��
��Ӧ�ı仯��Χ��
��![]() ���ܳ��Ƿ�һ����˵��������ɣ�
���ܳ��Ƿ�һ����˵��������ɣ�

���𰸡�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ʱ�ص����������С��
ʱ�ص����������С��![]() ��
��![]() ����
����![]() ���ܳ�һ�������ɼ�����.
���ܳ�һ�������ɼ�����.
��������
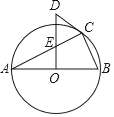
��1����Ϊ��B����A�غ�ʱ����A'B'C'������ABC������ת�����еĵ�һ����ȫ�غϣ�����=120�㣻
��2������A��B��C��������һ��������ABCƽ��ʱ�ص����������С���ɣ�1����֪��B����A�غ�ʱ����A'B'C'������ABC������ת�����еĵ�һ����ȫ�غ�ʱ��=60�������Ե���=60�㡢180����300��ʱ�ص����������С��
��3���������������εı߳���Ϊ6�����Ե�A��B����BCʱ����ADIΪ�ȱ������Σ�����ID=2������S��ADI=![]() IDAIsin60��=
IDAIsin60��=![]() ��2��2��
��2��2��![]() =
=![]() �������ɵó����ۣ�
�������ɵó����ۣ�
������AB��������AB=A'B'���ɵó�![]() ���ٸ���Բ�ܽǶ������ɵó�IA=IB'��DA=DA'�������ɵó����ۣ�
���ٸ���Բ�ܽǶ������ɵó�IA=IB'��DA=DA'�������ɵó����ۣ�
![]() �ߵ�
�ߵ�![]() ��
��![]() �غ�ʱ��
�غ�ʱ��![]() ����
����![]() ������ת�����еĵ�һ����ȫ�غϣ���ʱ��
������ת�����еĵ�һ����ȫ�غϣ���ʱ��![]() ��
��![]() �غϣ���ת�Ƕ�
�غϣ���ת�Ƕ�![]() ��
��
�൱![]() ʱ����
ʱ����![]() ����
����![]()
������ת�����еĵ�һ����ȫ�غϣ�
![]() ��
��![]() ������һ������
������һ������![]() ƽ��ʱ�ص����������С��
ƽ��ʱ�ص����������С��
����![]() ��֪��
��֪��![]() ��
��![]() �غ�ʱ��
�غ�ʱ��![]() ����
����![]() ������ת�����еĵ�һ����ȫ�غ�ʱ
������ת�����еĵ�һ����ȫ�غ�ʱ![]() ��
��
�൱![]() ��
��![]() ��
��![]() ʱ�ص����������С��
ʱ�ص����������С��
![]() �١��������εı߳���Ϊ
�١��������εı߳���Ϊ![]() ��
��
�൱![]() ʱ��
ʱ��![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ�
��![]() ��
��
��![]() ��
��
��![]() ���
���![]() ��Ӧ�ı仯��ΧΪ��
��Ӧ�ı仯��ΧΪ��![]()
��![]() ���ܳ�һ�����������£�
���ܳ�һ�����������£�
����![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
ͬ����![]() ��
��
��![]() ���ܳ���
���ܳ���![]() ��
��