题目内容
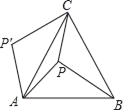
【题目】如图所示，
中，
，
，
．若有一半径为
的圆分别与
、
相切，则下列何种方法可找到此圆的圆心（ ）
A. 
的角平分线与
的交点
B. 的中垂线与中垂线的交点
C. 的角平分线与中垂线的交点
D. 的角平分线与中垂线的交点
【答案】D
【解析】
因为圆分别与AB、BC相切，所以圆心到AB、CB的距离一定相等，都等于半径．而到角的两边距离相等的点在角的平分线上，圆的半径为10，所以圆心到AB的距离为10．因为BC=20，所以BC的中垂线上的点到AB的距离为10，所以∠B的角平分线与BC的中垂线的交点即为圆心．
如图，
∵圆分别与AB、BC相切，
∴圆心到AB、CB的距离都等于半径，
∵到角的两边距离相等的点在角的平分线上，
∴圆心定在∠B的角平分线上，
∵因为圆的半径为10，
∴圆心到AB的距离为10，
∵BC=20，
又∵∠B=90°，
∴BC的中垂线上的点到AB的距离为10，
∴∠B的角平分线与BC的中垂线的交点即为圆心．
故选D．
练习册系列答案
课程达标测试卷闯关100分系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目
