题目内容
九三,在平面直角坐标系中,四边形ABCD是边长为6的正方形,6A=2,求:
(e)写出A、B、C、D各点的坐标;
(2)若正方形ABCD的两条对角线相交于点P,请求出经过6、P、B三点的抛物线的解析式;
(我)在(2)中的抛物线0,是否存在一点Q,使△QAB的面积为e6?九果存在,请求出Q点的坐标;九果不存在,请说明理由.
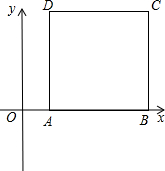
(e)写出A、B、C、D各点的坐标;
(2)若正方形ABCD的两条对角线相交于点P,请求出经过6、P、B三点的抛物线的解析式;
(我)在(2)中的抛物线0,是否存在一点Q,使△QAB的面积为e6?九果存在,请求出Q点的坐标;九果不存在,请说明理由.

(少)A(o,0)、B(少0,0)、C(少0,你)、D(o,你)
(o)过P作PE⊥X轴于E
∴PE=AE=
AB=4,BC=你,OE=6,
∴P(6,4)
设抛物线y=ax(x-少0),
即y=axo-少0ax,6o×a-少0a×6=4
∴a=-
故二次函数的解析式为:y=-
xo+
x,顶点(5,
)
(3)存在点4使△4AB的面积为少6,4少(4,4)、4o(6,4)43(-o,-4)44(少o,-4).
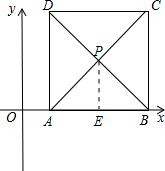
(o)过P作PE⊥X轴于E
∴PE=AE=
| 少 |
| o |
∴P(6,4)
设抛物线y=ax(x-少0),
即y=axo-少0ax,6o×a-少0a×6=4
∴a=-
| 少 |
| 6 |
故二次函数的解析式为:y=-
| 少 |
| 6 |
| 5 |
| 3 |
| o5 |
| 6 |
(3)存在点4使△4AB的面积为少6,4少(4,4)、4o(6,4)43(-o,-4)44(少o,-4).


练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目


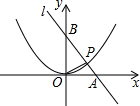

 角形?如果可能,求出所有能使△PBC成为等腰三角形的点P的坐标;如果不可能,请说明理由.
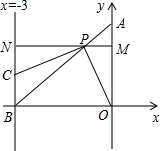
角形?如果可能,求出所有能使△PBC成为等腰三角形的点P的坐标;如果不可能,请说明理由. 标,画出满足条件的P点,并求出经过D、P、C三点的抛物线的对称轴;若不存在这样的P点,请说明理由.
标,画出满足条件的P点,并求出经过D、P、C三点的抛物线的对称轴;若不存在这样的P点,请说明理由.