题目内容
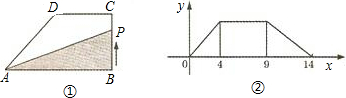
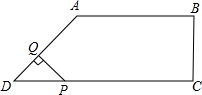 在直角梯形ABCD中,AB∥CD,BC⊥DC于点C,AB=2,CD=3,∠D=45°,动点P从D点出发,沿DC以每秒1个单位长度的速度移动,到C点停止.过P点作PQ垂直于直 线 AD,垂足为Q.设P点移动的时间为t秒,△DPQ与直角梯形ABCD重叠部分的面积为S,下列图象中,能表示S与t的函数关系的图象大致是( )
在直角梯形ABCD中,AB∥CD,BC⊥DC于点C,AB=2,CD=3,∠D=45°,动点P从D点出发,沿DC以每秒1个单位长度的速度移动,到C点停止.过P点作PQ垂直于直 线 AD,垂足为Q.设P点移动的时间为t秒,△DPQ与直角梯形ABCD重叠部分的面积为S,下列图象中,能表示S与t的函数关系的图象大致是( )A、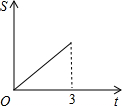 | B、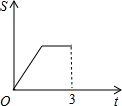 | C、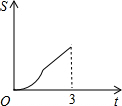 | D、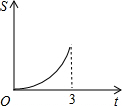 |
分析:此题属于分段函数,分为当Q在线段AD上时,(△DPQ与直角梯形ABCD重叠部分的面积为S就是△PDQ的面积)与当Q在线段DA的延长线时(此时△DPQ与直角梯形ABCD重叠部分的面积为S是两个三角形的面积差),分别求解即可求得函数解析式,则问题得解.
解答: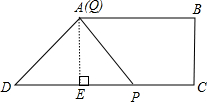 解:过点A作AE⊥CD于E,
解:过点A作AE⊥CD于E,
∵AB∥CD,BC⊥DC,
∴四边形AECB是矩形,
∴CE=AB=2,
∴DE=CD-CE=3-2=1,
∵∠D=45°,
∴AE=DE=1,AD=
,
∴当0≤t≤
时,
根据题意得:PD=t,则PQ=DQ=
t,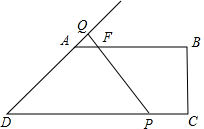
∴S△PDQ=
t•
t=
t2;
当
<t≤3时,
∵PD=t,则PQ=DQ=
t,AQ=FQ=
t-
,
S梯形AFPD=
t2-(
t-
)2=2t-2.
∴图象开始是抛物线,然后是直线.
故选C.
 解:过点A作AE⊥CD于E,
解:过点A作AE⊥CD于E,∵AB∥CD,BC⊥DC,
∴四边形AECB是矩形,
∴CE=AB=2,
∴DE=CD-CE=3-2=1,
∵∠D=45°,
∴AE=DE=1,AD=
| 2 |
∴当0≤t≤
| 2 |
根据题意得:PD=t,则PQ=DQ=
| ||
| 2 |

∴S△PDQ=
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
当
| 2 |
∵PD=t,则PQ=DQ=
| ||
| 2 |
| ||
| 2 |
| 2 |
S梯形AFPD=
| 1 |
| 2 |
| ||
| 2 |
| 2 |
∴图象开始是抛物线,然后是直线.
故选C.
点评:此题考查了梯形的性质,等腰直角三角形的性质以及勾股定理等知识.此题属于动点问题,解题的关键是分类讨论思想与数形结合思想的应用.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
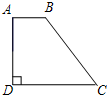 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,若AD=8,BC=10,则cosC的值为( )
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,若AD=8,BC=10,则cosC的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,且AB=BC=4AD,E是AB上的一点,DE⊥EC.求证:CE平分∠BCD.
如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,且AB=BC=4AD,E是AB上的一点,DE⊥EC.求证:CE平分∠BCD. 如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为
如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为 如图,在直角梯形ABCD中,若AD=5,点A的坐标为(-2,7),则点D的坐标为( )
如图,在直角梯形ABCD中,若AD=5,点A的坐标为(-2,7),则点D的坐标为( )